Stetigkeit und Differenzierbarkeit
Wesentlich leichter als die Ungleichungen lässt sich die zugehörige quadratische Gleichung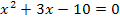 
lösen. Mit der Mitternachtsformel ergibt sich:
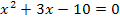
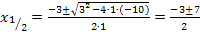
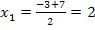
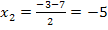
Jetzt haben wir leider noch immer nicht die quadratischen Ungleichungen gelöst. Das müssen wir jetzt aber machen. Bloßwie? Am leichtesten geht das graphisch. Wir stellen uns dabei die jeweils linke Seite der Ungleichungen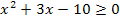 
und 
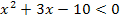als Parabel 
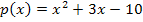vor.
Es handelt sich um eine nach oben geöffnete Normalparabel (Siehe auch:Quadratische Funktionen), die ihre Nullstellen bei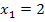 
und bei 
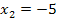hat. Die Nullstellen der Parabel 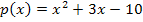haben wir nämlich oben gerade berechnet, als wir die quadratische Gleichung 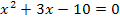gelöst haben. (Die Nullstellen, also die x-Koordinaten der Schnittpunkte mit der x-Achse, berechnet man schließlich, indem man die Funktion gleich Null setzt.) Mit Hilfe ihrer Nullstellen kann die Parabel 
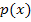grob skizziert werden. Wir wissen ja auch, dass die Parabel nach oben geöffnet ist, weil der Koeffizient a (d.h. die Zahl vor 
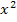) positiv ist. Bei 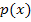handelt es sich sogar um eine Normalparabel, wegen a = 1. Die Breite der Parabel ist allerdings für die Lösungen der Ungleichungen irrelevant. Wichtig ist bloß, dass sie die Nullstellen bei 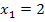und bei 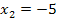hat und nach oben geöffnet ist.
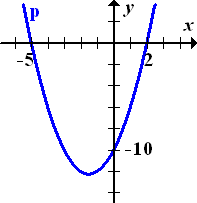
Abb.:Skizze der Parabel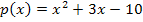
Doch wie entnimmt man jetzt dieser Zeichnung die Lösungen der beiden Ungleichungen 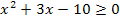und ?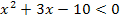
Wo die Parabel oberhalb der x-Achse verläuft bzw. die x-Achse schneidet, ist die Ungleichung 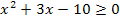, also 
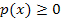erfüllt.
Wo die Parabel unterhalb der x-Achse verläuft, ist die Ungleichung 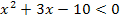, also 
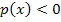erfüllt.
Du musst also nur die entsprechenden Bereiche auf der x-Achse ablesen.
Aus der Zeichnung entnehmen wir die Lösungen der Ungleichungen:
bzw.:
bzw.:
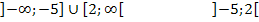
Nicht klar? Ok, dann ganz ausführlich bei:Ausführliche Erklärungen zur Lösung der quadratischen Ungleichungen im 2. Bsp.
Damit können wir nun die Funktion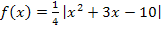 
endlich betragsfrei schreiben.
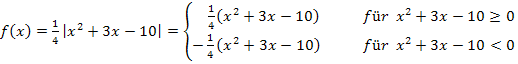
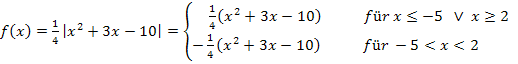
Oder alternativ dazu mit der Intervallschreibweise:
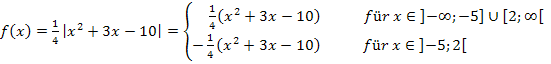
Eine andere mögliche Vorgehensweise zum Auflösen des Betrages:
Bei Funktionen, deren Gleichung komplett innerhalb eines Betrages stehen, erhält man den Graph der Betragsfunktion, indem man sich den Betrag erst einmal weg denkt und den Graph dieser Funktion (ohne Betrag) zeichnet;dann klappt man den unterhalb der x-Achse liegenden Teil einfach nach oben, man spiegelt ihn also an der x-Achse. Dadurch entsteht der Graph der Betragsfunktion. Aus dem Graph der Betragsfunktion lässt sich dann auf die betragsfreie Form der Funktionsgleichung schließen:In den Bereichen, wo nicht gespiegelt wurde, ersetzt man den Betrag durch Klammern. Bei den anderen Bereichen schreibt man statt dem Betrag eine Klammer mit Minus davor.
