Stetigkeit und Differenzierbarkeit
Wir vergleichen das Ergebnis mit dem schon vorher ermittelten linksseitigen Grenzwert der Ableitung:
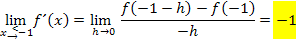
Der linksseitige und der rechtsseitige Grenzwert der Ableitung sind gleich. Die Funktion ist daher an der Stelle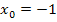 
differenzierbar. (Das haben wir oben ja auch schon mit der 1. Methode herausbekommen.)
Wie du an diesem Beispiel sehen konntest, ist die h-Methode sehr langwierig. Die andere Methode geht viel schneller. Leider musst du die h-Methode anwenden, wenn dein Lehrer in der Schule dies gemacht hat. Das betrifft vor allem Schüler der FOS. Schüler eines Gymnasiums dürfen in der Regel die 1. Methode verwenden. Das gilt auch für die Abiturprüfung. Wenn du unsicher bist, welche Methode du anwenden sollst, bitte deinen Mathe-Lehrer bzw. deine Lehrerin in der Schule fragen!
Da vor allem die h-Methode vielen Schülern anfangs Probleme bereitet, gleich noch ein weiteres Beispiel. Versuche es doch gleich alleine, bevor du dir die Lösung ansiehst! Wenn du allerdings Schwierigkeiten hast, die Funktion ohne Betrag zu schreiben, lies vorweg den Anfang der Lösung. Da wird erklärt, wie man den Betrag auflöst. Die Untersuchung der Differenzierbarkeit solltest du dann aber wirklich alleine rechnen.
2. Bsp.:Eine Betragsfunktion auf Differenzierbarkeit untersuchen
Die Funktion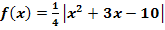 
mit 
ist in ihrer gesamten Definitionsmenge stetig. Untersuche die Differenzierbarkeit dieser Betragsfunktion! Liegt an den Nahtstellen jeweils ein Extremum vor? Wenn ja, welche Art von Extremum?
Lösung:
Vorweg muss die Funktion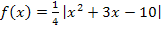 
betragsfrei geschrieben werden. Ist der Term, der innerhalb der Betragsstriche steht, positiv oder gleich Null, können die Betragsstriche durch eine Klammer ersetzt werden. Ist dieser Term dagegen negativ, müssen entweder alle Vorzeichen des Terms umgedreht werden und der Betrag dann durch eine Klammer ersetzt werden, oder man schreibt statt dem Betrag eine Klammer mit Minuszeichen davor. (Das Minuszeichen kommt dabei in diesem Beispiel aber ganz nach vorne, also vor 
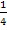und nicht dahinter!)
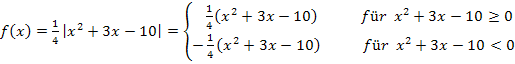
Jetzt stehen wir allerdings vor dem Problem, dass wir herausfinden müssen, für welche Werte von x der Ausdruck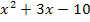 
positiv, negativ bzw. gleich Null ist. Es gilt also eigentlich die quadratischen Ungleichungen 
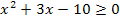und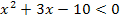 
zu lösen. (Dass wir hier das Gleichheitszeichen zum Größer Null hinzurechen und nicht zum Kleiner Null, ist reine Geschmackssache. Man hätte es auch genau umgekehrt machen können. Das Gleichheitszeichen darf aber grundsätzlich nur bei einer der beiden Ungleichungen dabei stehen und nicht bei beiden zugleich!)
