Stetigkeit und Differenzierbarkeit
Die Division durch Null ist ja nicht definiert. Um den Grenzwert zu berechnen, muss aber letztendlich für h genau die Zahl Null eingesetzt werden. Deshalb muss man bei der h-Methode immer im Zähler h ausklammern und danach h kürzen. Wenn du h nicht ausklammern kannst, weil noch eine Zahl ohne h im Zähler stehen geblieben ist, hast du dich hundertprozentig verrechnet. h muss sich hier immer ausklammern lassen. Das Prinzip der h-Methode haben wir ja auch schon bei der Herleitung der Tangentensteigung mittels des Differenzialquotienten behandelt. Siehe auch:Die h-Methode)
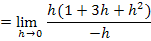
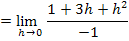
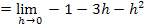
Nun kann der Grenzwert problemlos berechnet werden. Man muss nur noch für h die Zahl Null einsetzen. So ergibt sich:
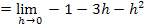
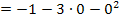
Nun haben wir den linksseitigen Grenzwert der Ableitung berechnet.
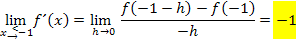
Den rechtsseitigen Grenzwert der Ableitung bilden wir mit dem allgemeinen Ansatz:
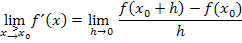
Hier noch einmal die Funktion: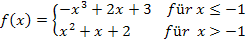 
Wir müssen die Differenzierbarkeit an der Nahtstelle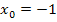 
überprüfen. Wir setzen daher für 
die Zahl -1 in den allgemeinen Ansatz ein. So ergibt sich:
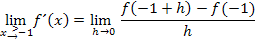
Das berechnet man folgendermaßen:Da wir uns jetzt von rechts an die Nahtstelle 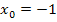annähern, müssen wir diejenige Teilfunktion verwenden, die für 
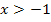gilt, also die untere Teilfunktion 
.
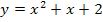Um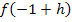 
zu bilden, musst du in dieser Teilfunktion jedes vorkommende x durch den Ausdruck 
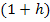ersetzen. 
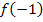müsste man streng genommen bilden, indem man in diejenige Teilfunktion, die bei 
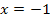gilt, für x die Zahl -1 einsetzt. Das wäre in diesem Beispiel die obere Teilfunktion, denn sie gilt für 
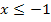. Da die Funktion 
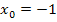an der Stelle aber sowieso stetig ist, spielt es keine Rolle, in welche Teilfunktion 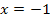eingesetzt wird. Man kann also auch die untere verwenden. Es kommt ja dasselbe Ergebnis heraus, ob man nun in die obere oder untere Teilfunktion für x die Zahl -1 einsetzt. Wir verwenden im Folgenden mathematisch korrekt die obere Teilfunktion 
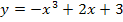, um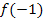 
zu berechnen.
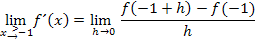
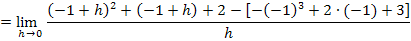
Vorsicht beim Vereinfachen von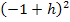 
. Beachte dabei: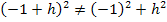 
Verwende am Besten zum Ausrechnen von 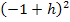die zweite Binomische Formel 
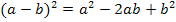Sie lässt sich anwenden, wenn man vorher die Reihenfolgen der Summanden in der Klammer von 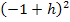vertauscht.
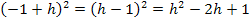
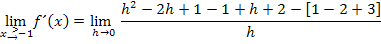
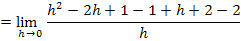
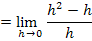
Nun klammern wir im Zähler wieder h aus, kürzen mit h und setzen dann für h die Zahl Null ein. So lässt sich der Grenzwert ab jetzt leicht berechnen.
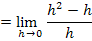
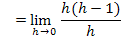
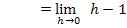
Nun haben wir auch den rechtsseitigen Grenzwert der Ableitung berechnet.
