Stetigkeit und Differenzierbarkeit
Nur wenn die Funktion dort differenzierbar ist, kann die Ableitung bei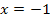 
gebildet werden und nur dann darf das Gleichheitszeichen wieder hinzugefügt werden. Wenn wir zeigen können, dass 
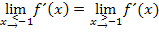gilt, dürfen wir statt 
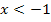wieder 
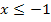bei der Ableitung der oberen Teilfunktion schreiben.
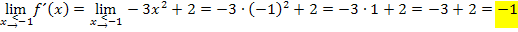
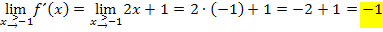
Es ergibt sich zweimal derselbe Wert. Es gilt also: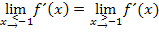
Die Funktion hat also bei Annäherung von links und von rechts an die Stelle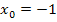 
die gleiche Steigung. (Dass sich bei diesem Beispiel für die Ableitung/Steigung der gleiche Wert wie 
ergibt, ist dabei reiner Zufall.)
Die Ableitung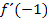 
ist definiert. Es gilt: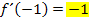 
Die Funktion 
ist somit an der Stelle 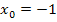differenzierbar. Der Graph 
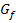hat keinen Knick;er verläuft „weich“. Weil die Ableitung 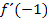definiert ist, darf nun auch wieder 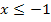statt 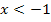bei der Ableitung der oberen Teilfunktion geschrieben werden.
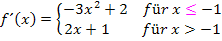
Im Prinzip ist die soeben gezeigte Methode völlig ausreichend, um die Differenzierbarkeit zu überprüfen. Doch manche Lehrer wollen stattdessen die h-Methode sehen. Also schauen wir uns auch noch an, wie das funktioniert.
2. Methode:Differenzierbarkeit mit h-Methode überprüfen
Hier noch einmal die Funktion: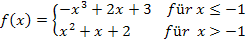 
Den linksseitigen Grenzwert der Ableitung bilden wir mit dem allgemeinen Ansatz:
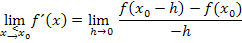
Dabei steht h für eine sehr kleine, positive Zahl. Es gilt also:h >0
Wir müssen die Differenzierbarkeit an der Stelle 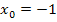überprüfen. Wir setzen daher für die Zahl -1 in den allgemeinen Ansatz ein. So ergibt sich:
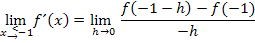
Wie rechnet man das jetzt aus? Ganz einfach:Weil wir uns der Nahtstelle 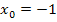von links nähern, müssen wir diejenige Teilfunktion nehmen, welche für 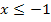gilt. Wir müssen deswegen als Funktionsterm die Teilfunktion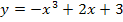 
verwenden, wenn wir 
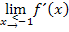berechnen wollen.
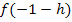bildest du, indem du in dieser Teilfunktion jedes x durch den Ausdruck 
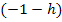ersetzt. 
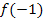berechnest du, indem du bei dieser Teilfunktion für x die Zahl -1 einsetzt.
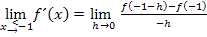
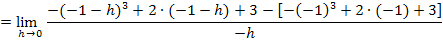
Den Ausdruck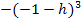 
kannst du z.B. in einer Nebenrechnung ausrechnen. Aber Vorsicht: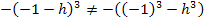 
Bedenke: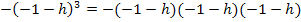 
Ausgerechnet ergibt sich: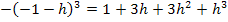 
Rechne das am besten gleich selbst nach! Am schnellsten geht die Rechnung mit Hilfe des Pascalschen Dreiecks. Dadurch ergibt sich die Formel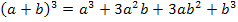 
. Um sie anwenden zu können, klammert man vorher -1, also ein Minus, aus:
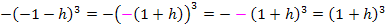
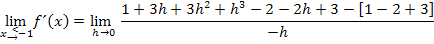
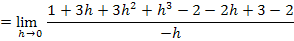
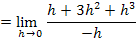
Im Zähler wir jetzt h ausgeklammert, damit man h danach aus dem Nenner komplett wegkürzen kann. (Solange h im Nenner steht, kann für h nicht Null eingesetzt werden.
