Stetigkeit und Differenzierbarkeit
Es liegt an der Stelle  ein Tiefpunkt vor. Stelle dir das einfach mit Pfeilen vor:
ein Tiefpunkt vor. Stelle dir das einfach mit Pfeilen vor:  Zuerst fällt der Graph, dann steigt er. Also ist hier ein Tiefpunkt bzw. Minimum.
Zuerst fällt der Graph, dann steigt er. Also ist hier ein Tiefpunkt bzw. Minimum.
Wenn die Vorzeichen der Grenzwerte genau umgekehrt sind, d.h. 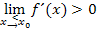 und
und 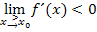 , liegt an der Stelle
, liegt an der Stelle  ein Hochpunkt / Maximum vor.
ein Hochpunkt / Maximum vor.
Obwohl die Steigung an der Knickstelle  nicht gleich Null ist, weil keine waagrechte Tangente vorhanden ist, existiert trotzdem ein Extremum, wenn an der Stelle
nicht gleich Null ist, weil keine waagrechte Tangente vorhanden ist, existiert trotzdem ein Extremum, wenn an der Stelle  ein Vorzeichenwechsel von
ein Vorzeichenwechsel von 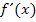 vorliegt.
vorliegt.
Also Vorsicht:Ist eine Funktion an einer Stelle nicht differenzierbar, hat sie dort einen Knick und es kann sein, dass genau an der Knickstelle ein Extremum liegt. Mit 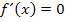 kannst du dieses Extremum nicht ermitteln!
kannst du dieses Extremum nicht ermitteln!
| Extremum an einer Knickstelle:
Eine Funktion ist an der Stelle · Haben die beiden Grenzwerte · Ob es sich um einen Hochpunkt oder Tiefpunkt handelt, kann nur an Hand der Monotonie / Steigungsverhaltens ermittelt werden, nicht aber mit Hilfe der zweiten Ableitung. |
Bevor wir uns ein Beispiel mit Extremum bei einem Knick des Graphen anschauen, wollen wir aber erst einmal an einem konkreten Beispiel zeigen, wie man die Differenzierbarkeit an einer bestimmten Stelle überprüft.
1. Bsp.:
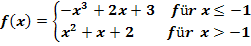
Überprüfe, ob die Funktion 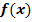 an der Stelle
an der Stelle 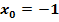 differenzierbar ist.
differenzierbar ist.
Lösung:
1. Schritt: Untersuchung der Stetigkeit
Es müssen die Grenzwerte der Funktion  für
für 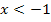 und
und 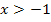 sowie der Funktionswert
sowie der Funktionswert 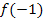 berechnet werden.
berechnet werden.
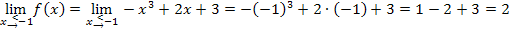
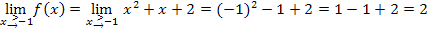
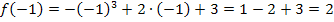
Es ergibt sich immer das gleiche Ergebnis. Daher ist die Funktion  an der Stelle
an der Stelle 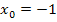 stetig.
stetig.
2. Schritt: Untersuchung der Differenzierbarkeit
1. Methode
Die Stetigkeit an der Stelle  ist nachgewiesen;nun leitet man die einzelnen Teilfunktionen mit Hilfe der Ableitungsregeln ab. (Siehe auch:Einfache Ableitungsregeln) Dann setzt man
ist nachgewiesen;nun leitet man die einzelnen Teilfunktionen mit Hilfe der Ableitungsregeln ab. (Siehe auch:Einfache Ableitungsregeln) Dann setzt man 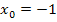 jeweils in die Ableitung der beiden Teilfunktionen ein. Ergibt sich dabei zweimal das gleiche Ergebnis, ist die Funktion an der Stelle
jeweils in die Ableitung der beiden Teilfunktionen ein. Ergibt sich dabei zweimal das gleiche Ergebnis, ist die Funktion an der Stelle 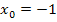 differenzierbar.
differenzierbar.
Hier noch einmal die Funktion:
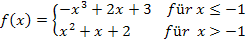
Erste Ableitung:
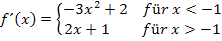
Vielleicht wunderst du dich, warum bei der Ableitung der oberen Teilfunktion nur 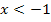 und nicht
und nicht 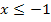 geschrieben wurde. Das ist kein Tippfehler, sondern Absicht! Wir wissen schließlich noch gar nicht, ob die Ableitung an der Stelle
geschrieben wurde. Das ist kein Tippfehler, sondern Absicht! Wir wissen schließlich noch gar nicht, ob die Ableitung an der Stelle 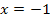 überhaupt existiert.
überhaupt existiert.

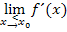 und
und 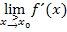 unterschiedliche Vorzeichen, dann liegt bei
unterschiedliche Vorzeichen, dann liegt bei 