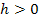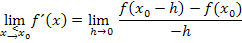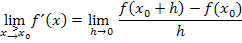Stetigkeit und Differenzierbarkeit
Die rechnerische Untersuchung der Differenzierbarkeit, also die Berechnung von 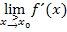 und
und 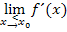 , kann auf zwei verschiedene Art und Weisen durchgeführt werden:Entweder mit der h-Methode oder einfacher durch Einsetzen von
, kann auf zwei verschiedene Art und Weisen durchgeführt werden:Entweder mit der h-Methode oder einfacher durch Einsetzen von  in die erste Ableitung sowohl der einen als auch der anderen Teilfunktion einer teilweise definierten Funktion.
in die erste Ableitung sowohl der einen als auch der anderen Teilfunktion einer teilweise definierten Funktion.
Anleitung zur rechnerischen Überprüfung der Differenzierbarkeit an der Stelle 
1. Methode: Einsetzten von · Ableitung der einzelnen Teilfunktionen mit Hilfe der Ableitungsregeln bilden · Links- und rechtsseitigen Grenzwert der Ableitung berechnen:
· Sind beide Ergebnisse gleich, ist die Funktion an der Stelle 2. Methode:Überprüfung der Differenzierbarkeit mit der h-Methode
h stellt im Folgenden irgendeine kleine, positive Zahl dar. Es gilt also:
· Linksseitigen Grenzwert der Ableitung bilden mit dem Ansatz:
· Rechtsseitigen Grenzwert der Ableitung bilden mit dem Ansatz:
· Sind beide Ergebnisse gleich, ist die Funktion an der Stelle |
Ist eine Funktion nicht differenzierbar an der Stelle  , so kann die Ableitung an dieser Stelle nicht angegeben werden.
, so kann die Ableitung an dieser Stelle nicht angegeben werden. 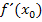 ist dann nicht definiert!
ist dann nicht definiert!
An einer Stelle, wo die Funktion nicht differenzierbar ist, d.h. bei einer Knickstelle, kann aber eventuell ein Extremum der Funktion vorliegen! Solche Extrema können nicht durch Gleichnullsetzen der Ableitung berechnet werden! Man erkennt solche Extrema nur am Vorzeichenwechsel der Ableitung, also daran, dass die Grenzwerte der Ableitung, die man bei der Überprüfung der Differenzierbarkeit berechnet hat, unterschiedliche Vorzeichen haben. (Wenn ein Extremum vorliegt, muss der Graph auf der einen Seite steigen und auf der anderen Seite fallen. Daher ändert sich am Extremum immer das Vorzeichen der Steigung, d.h. der Ableitung.)
Ist beispielsweise 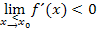 und
und 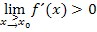 , bedeutet das, dass der Graph
, bedeutet das, dass der Graph 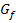 für
für 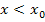 (also links von der Nahtstelle) streng monoton fallend und für
(also links von der Nahtstelle) streng monoton fallend und für 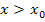 (also rechts von der Nahtstelle) streng monoton steigend ist.
(also rechts von der Nahtstelle) streng monoton steigend ist.

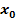 in die Ableitung der einzelnen Teilfunktionen
in die Ableitung der einzelnen Teilfunktionen