Stetigkeit und Differenzierbarkeit
Bei der Stetigkeit ging es immer um die Grenzwerte des Funktionswertes  , also um die y-Werte der Teilfunktionen an der Stelle
, also um die y-Werte der Teilfunktionen an der Stelle  . Bei der Differenzierbarkeit geht es dagegen um die erste Ableitung
. Bei der Differenzierbarkeit geht es dagegen um die erste Ableitung 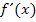 , also um die Steigung der Funktion bei Annäherung von links bzw. rechts an die Stelle
, also um die Steigung der Funktion bei Annäherung von links bzw. rechts an die Stelle  .
.
Soll eine Funktion  an der Stelle
an der Stelle  auf Differenzierbarkeit untersucht werden, muss der links- und rechtsseitige Grenzwert der Ableitung
auf Differenzierbarkeit untersucht werden, muss der links- und rechtsseitige Grenzwert der Ableitung 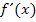 gebildet werden. Es geht hierbei somit um die Steigung an der Nahtstelle, also ob die von links und von rechts an den Graph gelegten Tangenten jeweils die gleiche Steigung besitzen.
gebildet werden. Es geht hierbei somit um die Steigung an der Nahtstelle, also ob die von links und von rechts an den Graph gelegten Tangenten jeweils die gleiche Steigung besitzen.
|
Definition: Eine an der Stelle
|
Anmerkung:
 ist eine konkrete Zahl. Eine Funktion wird immer lokal, also an einer bestimmten Stelle
ist eine konkrete Zahl. Eine Funktion wird immer lokal, also an einer bestimmten Stelle  auf Differenzierbarkeit untersucht. Im ersten nachfolgenden Beispiel (siehe unten) ist
auf Differenzierbarkeit untersucht. Im ersten nachfolgenden Beispiel (siehe unten) ist 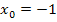 . Mit
. Mit  ist, wie schon bei der Stetigkeit, die Nahtstelle gemeint, d.h. die x-Koordinate des Punktes, wo die jeweiligen Teilfunktionen einer teilweise definierten Funktion zusammenstoßen.
ist, wie schon bei der Stetigkeit, die Nahtstelle gemeint, d.h. die x-Koordinate des Punktes, wo die jeweiligen Teilfunktionen einer teilweise definierten Funktion zusammenstoßen.
Oben gezeigte Definition noch einmal in Worten:Sind der linksseitige und der rechtsseitige Grenzwert der ersten Ableitung 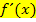 an der Stelle
an der Stelle 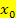 gleich, ist eine stetige Funktion an der Stelle
gleich, ist eine stetige Funktion an der Stelle 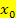 differenzierbar, d.h. sie hat dort keinen Knick. Die Teilfunktionen einer teilweise definierten Funktion gehen „weich“ ineinander über. Nur dann kann man die Steigung der Funktion an der Stelle
differenzierbar, d.h. sie hat dort keinen Knick. Die Teilfunktionen einer teilweise definierten Funktion gehen „weich“ ineinander über. Nur dann kann man die Steigung der Funktion an der Stelle  , d.h. ihre Ableitung
, d.h. ihre Ableitung 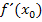 an dieser Stelle, angegeben.
an dieser Stelle, angegeben.
Wichtig:Bevor die Differenzierbarkeit an der Stelle 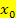 untersucht werden kann, muss die Stetigkeit gezeigt werden! Nur wenn in der Aufgabenstellung bereits angegeben ist, dass die Funktion an der zu untersuchenden Stelle stetig ist, kann auf die rechnerische Überprüfung der Stetigkeit verzichtet werden. Ansonsten gilt:Immer erst Stetigkeit zeigen, danach auf Differenzierbarkeit prüfen. (Ist die Funktion an der Stelle
untersucht werden kann, muss die Stetigkeit gezeigt werden! Nur wenn in der Aufgabenstellung bereits angegeben ist, dass die Funktion an der zu untersuchenden Stelle stetig ist, kann auf die rechnerische Überprüfung der Stetigkeit verzichtet werden. Ansonsten gilt:Immer erst Stetigkeit zeigen, danach auf Differenzierbarkeit prüfen. (Ist die Funktion an der Stelle  nicht stetig, dann ist sie auch nicht differenzierbar. Das braucht man gar nicht rechnerisch untersuchen, denn nur eine an der Stelle
nicht stetig, dann ist sie auch nicht differenzierbar. Das braucht man gar nicht rechnerisch untersuchen, denn nur eine an der Stelle  stetige Funktion kann dort überhaupt differenzierbar sein. Wenn eine Funktion eine Sprungstelle hat (also unstetig ist), kann ihr Graph an dieser Stelle schließlich nicht weich verlaufen (kann also gar nicht differenzierbar sein).
stetige Funktion kann dort überhaupt differenzierbar sein. Wenn eine Funktion eine Sprungstelle hat (also unstetig ist), kann ihr Graph an dieser Stelle schließlich nicht weich verlaufen (kann also gar nicht differenzierbar sein).
| Merke:
1. Schritt:Stetigkeit an der Stelle Ist die Funktion an der Stelle nicht stetig bei Ist die Funktion an der Stelle 2. Schritt:Differenzierbarkeit an der Stelle |

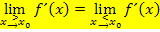
 nicht differenzierbar bei
nicht differenzierbar bei 