Stetigkeit und Differenzierbarkeit
„Kleiner“ bedeutet immer „weiter links auf dem Zahlenstrahl“, auch bei negativen Zahlen.)
Bsp.: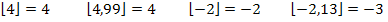 
p>
Den Graph der Funktion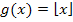 
kannst du in der nachfolgenden Abbildung sehen. Man erkennt sofort die Sprungstellen (Unstetigkeitsstellen) bei allen ganzzahligen Werten von x.
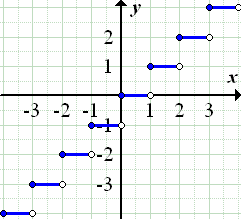
Abb.:Graph der (unteren) Gauß-Klammer-Funktion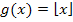
Die Gauß-Klammer-Funktion hat offensichtlich unendlich viele Unstetigkeitsstellen:Bei allen ganzen Zahlen ist die Funktion unstetig, sonst ist sie aber stetig. Auf den rechnerischen Nachweis dieser Tatsache wollen wir hier verzichten;das ist nichts für Schüler. (Wer sich für so etwas interessiert, muss Mathe als Hauptfach studieren. An der Uni wird das behandelt, aber nicht in der Schule.)
Es gibt aber, wie schon oben erwähnt, nicht nur Funktionen mit unendlich vielen Unstetigkeitsstellen, sondern auch Funktionen, die an gar keiner Stelle stetig sind. Ein Beispiel für eine Funktion, die überall unstetig ist, stellt die folgende Funktion dar:
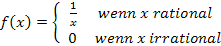
Da zwischen zwei rationalen Zahlen (d.h. Brüchen bzw. Dezimalzahlen) unendlich viele irrationale Zahlen liegen (d.h. Zahlen, die sich nicht als endliche Dezimalzahl oder Bruch schreiben lassen, wie zum Beispiel Wurzeln, die nicht aufgehen), gibt es hier unendlich viele Unstetigkeitsstellen. Der Term 
kann nämlich für keine rationale Zahl x den Wert 0 annehmen. Für rationale x ergibt sich somit immer ein Funktionswert ungleich 0, wogegen für alle irrationalen x der Funktionswert 0 herauskommt. Die Funktionswerte springen also ständig zwischen Zahlen ungleich Null und der Zahl Null hin und her. Die Funktion ist nirgendwo stetig! Den rechnerischen Nachweis wollen wir hierfür allerdings auf dieser website nicht erbringen;es wäre zu kompliziert. (Das wird auch erst im Hauptstudium Mathe verlangt.) Wirklich exakt zeichnen lässt sich der Graph dieser Funktion nicht. Er besteht im Prinzip aus unendlich vielen Einzelpunkten, die teils auf der x-Achse liegen (wenn x irrational ist) und nicht auf der x-Achse, sondern bei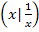 
liegen (wenn x rational ist). Wenn du dir das nicht wirklich vorstellen kannst, ist das nicht schlimm. Für Prüfungen an Gymnasien oder auf der FOS/BOS kommt so etwas bestimmt nicht dran. Es sollte nur als interessanter Ausblick für die Hochschulmathematik dienen. Erst im Studium mit Hauptfach Mathematik oder Wirtschaftsmathematik werden solche Funktionen rechnerisch auf Stetigkeit untersucht. Uns würde das aber zu weit führen.
2b.) Rechnerische Überprüfung der Differenzierbarkeit
