Stetigkeit und Differenzierbarkeit
Die Nahtstelle zwischen der obersten und der mittleren Teilfunktion liegt deshalb bei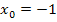 
. Die zweite Nahtstelle (zwischen der mittleren und der untersten Teilfunktion) liegt bei 
. (Anmerkung:Es ist hier zweimal die Bezeichnung 
gewählt worden, obwohl es sich natürlich um zwei verschiedene Stellen handelt. Einmal ist 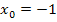und einmal . Das ist natürlich nicht ganz mathematisch korrekt. Eigentlich müsste die zweite Nahtstelle anders benannt werden, z. B.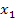 
. Du bist aber bestimmt inzwischen an die Bezeichnung für die Nahtstelle gewohnt. Daher nennen wir beide Nahtstellen allgemein . Es müssen aber zwei getrennte Rechnungen durchgeführt werden:Einmal die Untersuchung der Stetigkeit an der ersten Nahtstelle 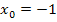und einmal an der zweiten Nahtstelle .)
Es wird in diesem Beispiel nur die schnelle Methode gezeigt;die h-Methode dauert einfach zu lang.
Untersuchung der Stetigkeit an der ersten Nahtstelle :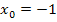
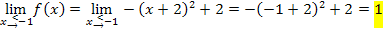
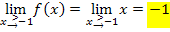
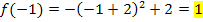
Die drei Ergebnisse sind nicht gleich;die Funktion 
ist somit an der Stelle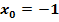 
nicht stetig.
Untersuchung der Stetigkeit an der zweiten Nahtstelle :
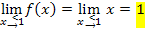
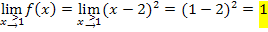
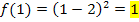
Die Ergebnisse sind alle drei gleich;die Funktion ist somit an der Stelle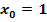 
stetig.
Damit ist die Aufgabe gelöst.
Damit du dir das Ganze besser vorstellen kannst, hier noch der Graph von . Er ist offensichtlich an der Stelle 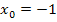unstetig, weil er dort eine Sprungstelle hat:Das linke Parabelstück stößt bei 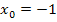nicht mit der Geraden zusammen. An der Stelle ist die Funktion dagegen stetig, da sich dort keine Sprungstelle befindet:Die Gerade stößt mit dem rechten Parabelstück im Punkt (1|1) exakt zusammen.
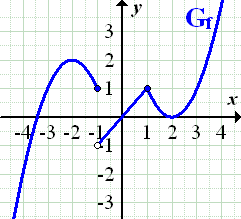
Abb.:Graph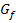 
der Funktion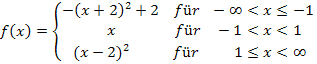 
Ausblick:
Neben den Funktionen, die an endlich vielen Stellen unstetig sind, gibt es interessanterweise auch welche, die an unendlich vielen Stellen oder sogar überall unstetig sind.
Ein Beispiel für eine Funktion mit unendlich vielen Unstetigkeitsstellen ist die Funktion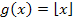 
. (Sprich:„Untere Gauß-Klammer von x“) Sie ist benannt nach Carl Friedrich Gauß, einem berühmten deutschen Mathematiker. Die Funktion 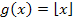ordnet jeder ganzen Zahl x, die Zahl selbst zu, und jeder anderen Zahl x die nächstkleinere ganze Zahl. Die Gauß-Klammer schneidet somit bei positiven Zahlen eventuell vorhandene Reste hinter dem Komma einfach ab. Bei negativen Zahlen wird aber wirklich die nächstkleinere ganze Zahl zugeordnet. (Vorsicht bei negativen Zahlen!
