Stetigkeit und Differenzierbarkeit
Hier noch einmal alle Ergebnisse übersichtlich zusammengefasst:
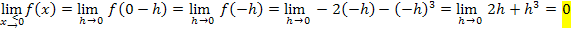
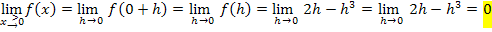
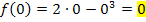
Wir erhalten natürlich wieder dreimal dasselbe Ergebnis;die Funktion ist somit stetig an der Stelle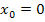 
. (Das haben wir ja auch schon mit der 1. Methode herausgefunden.)
3. Bsp.:Signum-Funktion
Die Signum-Funktion (lat. Signum = Vorzeichen, Zeichen)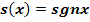 
ist folgendermaßen definiert:
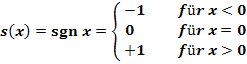
Die Signum-Funktion ordnet also jeder negativen Zahl den Wert -1 zu, jeder positiven Zahl den Wert +1. Der Zahl 0 wird die 0 zugeordnet. Die Signum-Funktion ist an der Stelle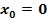 
unstetig, denn es gilt: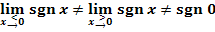 
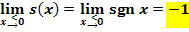
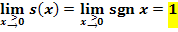
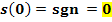
Untersuche rechnerisch, ob die Funktion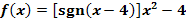 
an der Stelle 
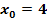stetig ist!
Lösung:
Als erstes schreiben wir die Funktion 
ohne Signum.
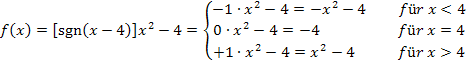
Dir ist nicht klar, wie das gemacht wurde, also wie man ohne Signum schreibt? Dann gehe zu:Ausführliche Erklärung zum Auflösen von sgn im 3. Bsp.
1. Methode:
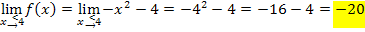
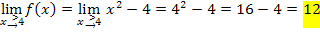
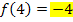
Es ergibt sich jedes Mal ein anderes Ergebnis. Daher ist die Funktion bei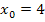 
nicht stetig. Der Graph 
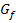hat also eine Sprungstelle bei .
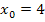2. Methode:
Hier noch einmal die Funktion:
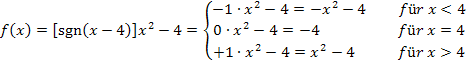
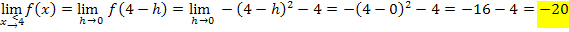
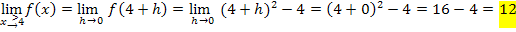
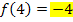
Wir erhalten natürlich wieder drei verschiedene Ergebnisse;die Funktion ist somit nicht stetig an der Stelle 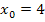. (Das haben wir ja auch schon mit der 1. Methode herausgefunden.)
Bisher haben wir uns ausschließlich mit Funktionen beschäftigt, die nur an einer einzigen Stelle auf Stetigkeit untersucht werden mussten. So war zum Beispiel die Funktion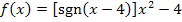 
nur an der Stelle 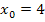unstetig. Natürlich gibt es auch Funktionen, die an zwei oder mehr verschiedenen Stellen unstetig sind. Das kann der Fall sein, wenn eine Funktion aus drei Teilfunktionen zusammengesetzt ist. Dann gibt es nämlich zwei Nahtstellen, wo die Funktion jeweils einzeln auf Stetigkeit untersucht werden muss. So eine Funktion wird im nächsten Beispiel behandelt. Funktionen, die zwei Nahtstellen haben, können entweder an beiden Stellen stetig, an beiden unstetig oder auch an einer Nahtstelle unstetig und an der anderen stetig sein. Genau das gilt es dann herauszufinden.
4. Bsp.:
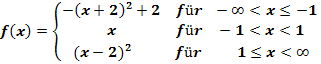
Untersuche die Funktion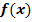 
auf Stetigkeit!
Lösung:
Die Funktion ist aus drei verschiedenen Teilfunktionen zusammengesetzt;es gibt daher zwei Nahtstellen. Die oberste Teilfunktion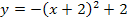 
gilt links von -1 und an der Stelle 
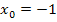. Die mittlere Teilfunktion 
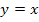gilt von -1 bis 1;die Zahlen -1 und 1 sind dabei jeweils ausgeschlossen. Für Zahlen größer oder gleich 1 gilt die unterste Teilfunktion 
.
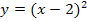