Stetigkeit und Differenzierbarkeit
Es darf aber nur bei einer der beiden Teilfunktionen, also entweder bei der oberen oder bei der unteren dazu geschrieben werden, nicht bei beiden gleichzeitig. An der Stelle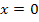 
soll genau eine Teilfunktion gelten, welche ist dabei egal. Wir haben hier bei der oberen Teilfunktion 
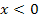und bei der unteren 
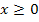geschrieben. Es wäre aber auch korrekt bei der oberen 
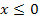und dafür bei der unteren 
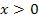zu schreiben.
Die Nahtstelle der beiden Teilfunktionen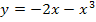 
und 
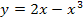liegt also bei 
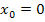, da die eine für 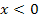und die andere für 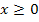gilt. Daher muss die Stetigkeit auch genau an der Stelle 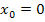überprüft werden. Wir wollen uns die beiden dafür möglichen Methoden anschauen.
1. Methode:Einsetzten von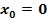 
in die beiden Teilfunktionen
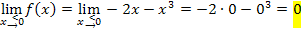
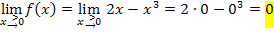
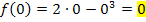
Es ergibt sich jedes Mal dasselbe Ergebnis. Daher ist die Funktion 
bei 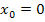stetig. Der Graph hat also keine Sprungstelle bei .
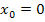2. Methode:Überprüfung der Stetigkeit mit der „h-Methode“
Hier noch einmal die Funktion in ihrer betragsfreien Form: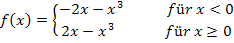 
Allgemeiner Ansatz der h-Methode für die Annäherung von links an die Stelle 
:
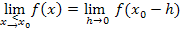
In dieser Aufgabe gilt: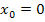
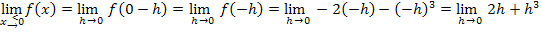
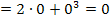
Anmerkung:Um in diesem Beispiel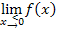 
, also 
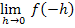zu berechnen, muss die Teilfunktion 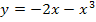verwendet werden, da man sich schließlich von links an die Nahtstelle annähert und diese Teilfunktion für 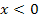gilt. Man ersetzt dann jedes x, das in 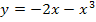vorkommt, durch 
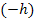. Danach vereinfacht man soweit möglich und setzt letztendlich für h die Zahl 0 ein.
Allgemeiner Ansatz der h-Methode für die Annäherung von rechts an die Stelle :
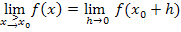
In dieser Aufgabe gilt: 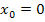und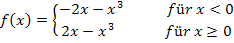
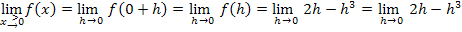
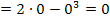
Anmerkung:Um in diesem Beispiel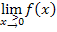 
, also 
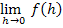zu berechnen, muss die Teilfunktion 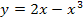verwendet werden, da man sich schließlich von rechts an die Nahtstelle annähert und diese Teilfunktion für 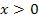gilt. Man ersetzt dann jedes x, das in 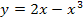vorkommt, durch h. Danach vereinfacht man soweit möglich und setzt letztendlich für h die Zahl 0 ein.
Der Funktionswert an der Stelle 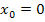wird berechnet, indem man in diejenige Teilfunktion, bei der man 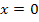eingeschlossen hat, für x die Zahl 0 einsetzt. (Da wir die Funktion selbst betragsfrei schreiben mussten, konnten wir selbst entscheiden, bei welcher Teilfunktion wir 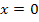miteinschließen. Wir hatten uns hier dafür entschieden, 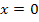zur unteren Teilfunktion 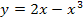zu zählen;wir haben schließlich festgelegt, dass 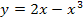für 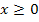gelten soll. Deshalb muss bei uns die Zahl 
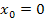in diese Teilfunktion für x eingesetzt werden, um f (0) zu bilden.)
