Welchen Ansatz bei welchen Aufgaben verwenden

Das 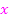lässt sich dabei weg kürzen;es ergibt sich somit: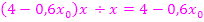 

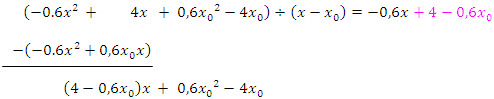
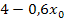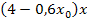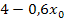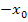Wie üblich bei der Polynomdivision, multiplizieren wir zurück: mal x genommen ergibt natürlich wieder , außerdem mal genommen ergibt: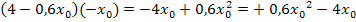

Das Ergebnis ziehen wir dann wieder ab.

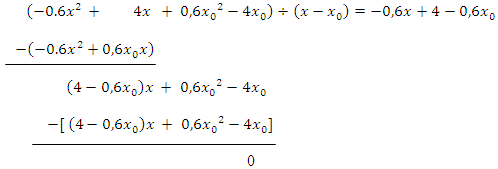
Die Polynomdivision ist aufgegangen! Spitze! Daran erkennst du, dass noch alles stimmt. Die Polynomdivision muss hierbei zwangsläufig aufgehen. Wenn dir also ein Rest übrig bleibt, weißt du, dass du dich irgendwo verrechnet haben musst. (Meistens liegt der Fehler in einem Vorzeichen;vor allem beim Subtrahieren negativer Ausdrücke bzw. Zahlen passieren vielen Schülern Vorzeichenfehler. Suche zuerst genau an diesen Stellen nach deinem Fehler!)

Wir haben durch die gezeigte Polynomdivision den Bruch 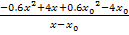ausgerechnet und können nun stattdessen das Ergebnis der Polynomdivision 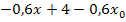hinter den Limes schreiben.

Daher gilt:

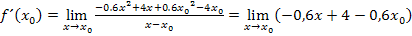
Nun kann der Grenzwert endlich berechnet werden. Das funktioniert vom Prinzip her wie schon oben bei der 1. Methode erklärt:Einfach für x einsetzen und so weit möglich zusammenfassen. (Dann natürlich nicht mehr 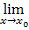schreiben.) Das Einsetzen von für x ist jetzt problemlos möglich;es gibt schließlich keinen Nenner mehr, der Null werden könnte.

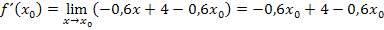
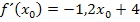
Es ergibt sich natürlich wieder dasselbe Ergebnis, wie schon oben bei der 1. Methode.

Als letztes ersetzen wir rein formal durch x, um von 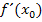auf die gesuchte Ableitungsfunktion 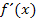zu kommen.

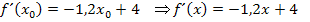
Dies ist die gesuchte Ableitung der Funktion .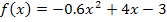

Wie du sehen konntest, sind beide Methoden ziemlich schwierig. Mit dem Differenzialquotienten in der Form 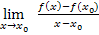lässt sich bei Funktionen mit 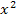und x sowie unbekanntem leider wirklich nicht gut rechnen. Es empfiehlt sich dann eher die Verwendung der h-Methode, welche bei Funktionen mit 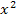und x sowie unbekanntem deutlich einfacher ist. Nur wenn ihr im Unterricht weder die h-Methode durchgenommen habt noch die Delta-x-Methode,d.h. den Differenzialquotienten in der Form 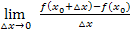, solltest du 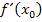bzw. 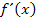nach der oben gezeigten umständlichen 1. oder 2. Methode ermitteln. Sowohl die 1. Methode als auch die 2. Methode stellen reine Notlösungen dar für Schüler, die im Unterricht wirklich nur mit dem Differenzialquotienten in der Form 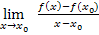gearbeitet haben. Diese Art der Berechnung von 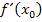bzw. 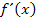ist an sich viel zu umständlich.
Doch leider gibt es immer ´mal wieder einzelne Lehrer, die dennoch genau eine dieser Methoden verlangen, auch wenn es anders viel einfacher ginge. Zum Trost sei allerdings gesagt, dass ihr im Unterricht sicher bald die sogenannten Ableitungsregeln lernt;damit kann man eine Funktion ganz schnell und ohne großen Rechenaufwand ableiten. Mehr dazu bei:Einfache Ableitungsregeln

---