Welchen Ansatz bei welchen Aufgaben verwenden

Anmerkung des Autors:Ich persönlich bevorzuge daher bei Funktionen mit 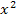und x im Allgemeinen die 2. Methode mit der Polynomdivision. Letztendlich musst du jedoch selbst entscheiden, was dir besser liegt, denn auch die Polynomdivision hat hier so ihre Tücken.

2. Methode:Verwendung einer Polynomdivision

Mit 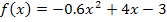hat sich nach dem Einsetzen in den Differenzialquotienten 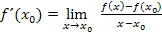und anschließendem Zusammenfassen ergeben:

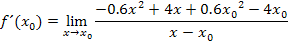
Um den Grenzwert berechnen zu können, wird der Bruch mit Hilfe einer Polynomdivision ausgerechnet. Wir sehen den Bruchstrich des Differenzialquotienten als normales Geteilt-Zeichen an. Das bedeutet, es muss folgende Polynomdivision durchgeführt werden:

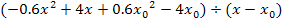
Diese Polynomdivision wird auf jeden Fall aufgehen. (Wenn sie bei dir einmal nicht aufgeht, hast du dich hundertprozentig irgendwo verrechnet.)

Die Polynomdivision funktioniert in diesem Beispiel folgendermaßen:

1. Schritt der Polynomdivision:

Zu Beginn muss wie üblich vorgegangen werden, d.h. es muss hier 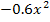durch x geteilt werden. Du kannst dich stattdessen auch fragen:x mal was ergibt 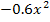? Die Antwort ist natürlich: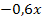

Dann wird wieder zurück multipliziert. Dadurch ergibt sich das folgende Zwischenergebnis.

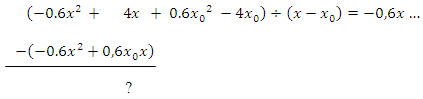
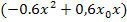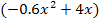Nun muss von subtrahiert werden. Klar ist bestimmt der vordere Teil: 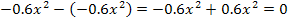Das hebt sich natürlich weg – muss es ja auch, sonst hätten wir einen Fehler beim vorherigen Dividieren gemacht. Doch jetzt stehst du vermutlich vor dem Problem, dass du nicht weißt, wie man von 4x den Ausdruck 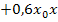abzieht. Logisch ist zwar bestimmt noch, dass das Abziehen von  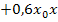 eigentlich bedeutet, das Vorzeichen dabei umzudrehen. Wir müssen also rechnen:

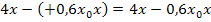
Das Blöde daran ist nur, dass hier noch dabei steht. Der Ausdruck 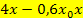lässt sich nur durch das Ausklammern von x zusammenfassen. Ausnahmsweise schreiben wir das x nach hinten, also hinter die Klammer.

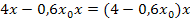
Damit ergibt sich nach dem 1. Schritt bei der Polynomdivision:

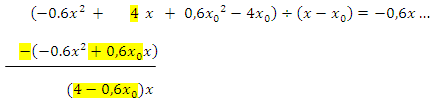
2. Schritt der Polynomdivision:

Du weißt bestimmt:Man muss bei der Polynomdivision immer genau denjenigen Teil aus der vorderen Klammer von ganz oben herunterholen, der eine um 1 niedrigere Potenz hat wie das, was gerade unterhalb des waagrechten Strichs steht. Bei uns steht momentan 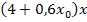bzw. 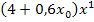unterhalb des waagrechten Strichs. Wir müssen deshalb alles herunterholen, was 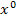als Potenz, also kein x enthält, d.h. hier den kompletten Term .

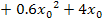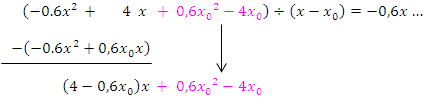
Dann starten wir die nächste Runde der Polynomdivision.

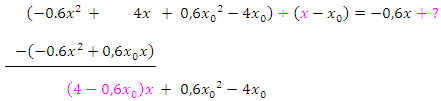
Es muss jetzt der Term 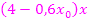durch 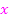dividiert werden.

---