Welchen Ansatz bei welchen Aufgaben verwenden
Damit ergeben sich die beiden Lösungen der Gleichung:
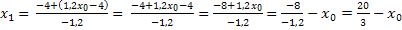
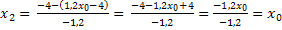
Da es zwei Lösungen gibt, gibt es auch zwei Linearfaktoren. Sie lauten in diesem Fall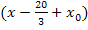 
und 
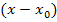. Hinter dem x in der Klammer steht bei den Linearfaktoren jeweils eine der berechneten Lösungen aber mit umgedrehten Vorzeichen.
· Faktorisierung des Zählers des Differenzialquotienten:
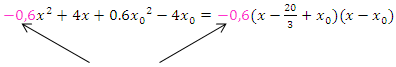
Die Zahl vor der höchsten Potenz von xmuss bei der faktorisierten Form mit den beiden Linearfaktoren multipliziert werden. Man muss also diese Zahl, hier -0,6, vor die beiden Linearfaktoren schreiben. Das darfst du nicht vergessen!
Daher können wir nun den gesamten Differenzialquotienten in seiner faktorisierten Form schreiben:
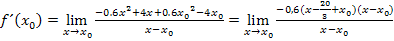
Jetzt kann man den Term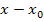 
endlich weg kürzen. Dadurch ergibt sich:
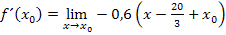
Nun kann der Grenzwert berechnet werden. Man muss nur noch 
für x einsetzen. (Dann natürlich nicht mehr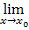 
schreiben.) Das Einsetzen von für x ist jetzt problemlos möglich;es gibt ja keinen Nenner mehr, der Null werden könnte.
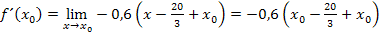
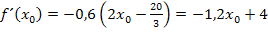
Als letztes ersetzen wir rein formal durch x, um von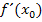 
auf die gesuchte Ableitungsfunktion 
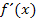zu kommen.
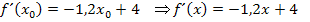
Dies ist die gesuchte Ableitung der Funktion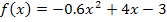 
.
Ein wirklich hilfreicher Tipp:
Wenn du das Ergebnis von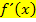 
schnell im Kopf überprüfen willst, musst du nur folgendes machen:Bei jeder x-Potenz von 
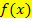den Exponenten nach vorne ziehen und mit der Zahl davor multiplizieren, außerdem die Zahl 1 vom Exponenten abziehen. Zahlen ganz ohne x fallen ganz weg, weil man sich zu einer Zahl ohne x einfach 
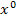dazu denken kann und Null mit etwas multipliziert ergibt Null, fällt also weg. So kannst du 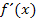ganz leicht im Kopf ermitteln.
Kontrolle:
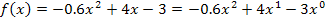
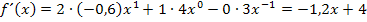
Super, das Ergebnis stimmt mit dem überein, das wir oben mit viel Mühe mit dem Differenzialquotienten gebildet haben. Es stimmt somit alles. (Ausführlichere Erläuterungen zu der Schnellmethode, mit der wir soeben 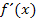im Kopf gebildet haben, findest du im Abschnitt:Einfache AbleitungsregelnLeider darfst du dieses Verfahren offiziell erst später anwenden.)
Wie du an diesem Beispiel sehen konntest, ergibt sich bei der Berechnung des Differenzialquotienten bei Funktionen mit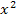 
und x das Problem, dass sich der Nenner erst nach schwieriger Rechnung kürzen lässt. Das Faktorisieren des Zählers dauert bei solchen Funktionen sehr lange und ist echt nicht einfach. Leider kann der Nenner erst dann weggekürzt werden, wenn der Zähler vollständig faktorisiert ist.
