Welchen Ansatz bei welchen Aufgaben verwenden
Deshalb machen wir das am besten gemeinsam. (Es reicht an sich, wenn du nur eine der beiden folgenden Rechnungen nachher selbstständig durchführen kannst. Im Folgenden werden hier beide Methoden vorgeführt, damit du dir diejenige heraussuchen kannst, die dir persönlich besser liegt.)
1. Methode:Faktorisieren und danach Kürzen
Hinweis:Wenn du nicht mehr weißt, wie ein Term faktorisiert werden kann, siehe auch Faktorisierter Funktionsterm!
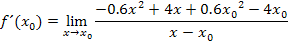
Wir müssen den Ausdruck, der sich im Zähler des Differenzialquotienten befindet, vollständig faktorisieren, also in diesem Fall den Ausdruck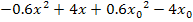 
. Da sich in diesem Fall weder x ausklammern noch eine binomische Formel anwenden lässt, bleibt uns nur die folgende Methode:
· Gleich Null setzen:
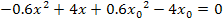
Die Gleichung enthält leider neben der Unbekannten x und deren Quadrat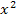 
auch noch 
. Wichtig: steht dabei für eine unbekannte, aber feste Zahl. Du musst deshalb wie eine ganz normale Zahl behandeln. Dem entsprechend ist die vorliegende Gleichung gemischt-quadratisch mit der Unbekannten x, d.h. sie hat die Form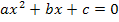 
. Solche Gleichungen lassen sich bekanntlich mit der Mitternachtsformel lösen. Doch was entspricht in diesem Fall den Koeffizienten a, b und c?
a dürfte klar sein:a ist schließlich einfach die Zahl vor dem 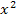, also gilt hier:a = -0,6 Auch b macht dir bestimmt keine Probleme, denn b entspricht immer der Zahl vor dem x (ohne Quadrat). Daher gilt hier:b = 4
Und was ist jetzt mit c? Ganz einfach:Alles, was kein x enthält, entspricht dem c. In diesem Fall gilt also: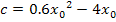 
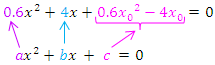
· Mitternachtsformel: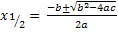 
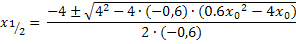
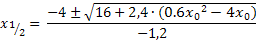
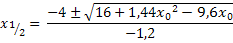
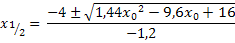
Und jetzt? Wie du weißt, darf man bei einer Summe oder Differenz die Wurzel nicht aus jedem Summanden einzeln ziehen. Hier steht aber unter der Wurzel ein Ausdruck mit Plus bzw. Minus, also eine Summe bzw. Differenz;wir dürfen die Wurzel daher nicht aus jedem Summanden einzeln ziehen. In der obigen Form stehen lassen können wir das Ganze auch nicht;wir wollen schließlich den Zähler des Differenzenquotienten faktorisieren und mit dem bisherigen Ergebnis klappt das bestimmt nicht. Hast du selbst eine Idee, was man mit dem Ausdruck unter der Wurzel machen kann?
Kleiner Tipp: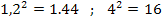 
Hoffentlich hast du erkannt, dass sich bei dem Ausdruck unter der Wurzel die zweite binomische Formel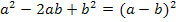 
anwenden lässt? Es gilt daher:
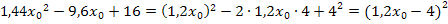
Damit ergibt sich:
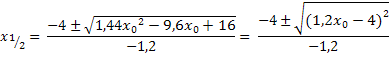
Jetzt können wir die Wurzel endlich ziehen, denn Wurzel und Quadrat heben sich gegenseitig auf:
