Welchen Ansatz bei welchen Aufgaben verwenden
Der Differenzialquotient ist bloßeine Hinführung zum Thema Ableitung einer Funktion. Zum Ableiten einer gegebenen Funktion können nämlich auch die sogenannten Ableitungsregeln verwendet werden. Ihr werdet die Ableitungsregeln bestimmt gleich im Anschluss an den Differenzialquotienten im Unterricht behandeln. Damit kannst du deine Ergebnisse, die du mit dem Differenzialquotienten berechnet hast, selbst leicht kontrollieren. Mehr dazu bei:Einfache Ableitungsregeln
Sehr schwieriges Beispiel zum Differenzialquotienten mit Variante 3
Wir betrachten die folgende Funktion: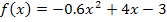 
Es soll die Ableitungsfunktion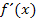 
mit dem Differenzialquotienten in der Form 
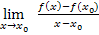berechnet werden. Dazu muss man vorweg die Ableitung 
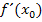an einer festen Stelle 
berechnen. Erst danach kann dann rein formal durch x ersetzt werden. Dadurch erhält man die gesuchte Ableitungsfunktion 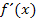. Der Funktionsterm von 
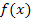enthält aber neben 
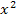auch ein x (ohne Potenz);das führt uns zu einer besonderen Problematik bei der Berechnung des Differenzialquotienten mit diesem Ansatz. Welche Problematik das ist, wirst du gleich selbst sehen. Versuche einfach ´mal alleine 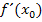mit der gegebenen Funktion und dem erwähnten Ansatz zu ermitteln. Was ergibt sich dann?
Hoffentlich hast du es inzwischen alleine versucht. Dann müsstest du auf Folgendes gekommen sein:
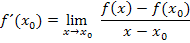
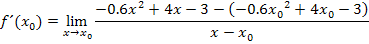
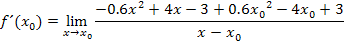
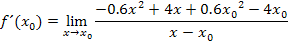
So, und jetzt? Wie geht es nun weiter? Man muss irgendwie den Ausdruck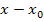 
aus dem Nenner weg bekommen, aber es lässt sich im Zähler keine binomische Formelanwenden und auch die Polynomdivision wird hier schwierig werden, weil ja neben der Variablen x auch noch vorkommt. steht zwar für eine feste Zahl, doch wir kennen diese Zahl nicht und deshalb können wir nichts Konkretes für einsetzen. Das ist also das oben erwähnte Problem. Solange 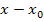im Nenner steht, kann man aber nicht für x einsetzen, weil dann schließlich der Nenner gleich Null werden würde. Der Ausdruck 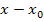muss also weg aus dem Nenner. Bloßwie macht man das in diesem Fall?
Wie sind wir denn vorgegangen, wenn gegeben war, sich aber zum Faktorisieren des Zählers keine binomische Formel anwenden ließ? Da hatten wir die zwei folgenden Möglichkeiten:
1. Zähler faktorisieren und dann 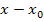kürzen
2. Polynomdivision (Zähler durch Nenner teilen)
Genau diese beiden Möglichkeiten stehen uns auch in diesem Fall zur Verfügung. Allerdings ist die Rechnung bei beiden Möglichkeiten mit unbekanntem viel schwieriger als bei bekanntem .
