Welchen Ansatz bei welchen Aufgaben verwenden
Bei Funktionen der Form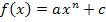 
klappt deshalb die Variante 3 wirklich gut. Das sollte dir klar geworden sein, wenn du dich mit Variante 3 genauer beschäftigt hast.
Bei der Delta-x-Methode muss bei der Berechnung des Differenzialquotientens im Zähler immer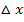 
ausgeklammert werden. (Das ist oft einfacher als die Polynomdivision bzw. Faktorisierung des Zählers in Variante 3.) Anschließend wird dann 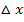gekürzt und der Grenzwert berechnet, indem man 0 für 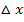einsetzt.
Entsprechend wird bei der h-Methode im Zähler erst h ausgeklammert, damit sich anschließend h kürzen lässt. (Siehe auch:Die h-Methode) Nachher wird dann 0 für h eingesetzt, um den Grenzwert zu berechnen.
Bei Variante 3 wird entweder der Zähler des Differenzialquotientens vollständig faktorisiert und anschließend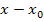 
weg gekürzt oder stattdessen eine Polynomdivision (Zähler durch Nenner des gebildeten Differenzialquotientens) durchgeführt. Danach wird dann für x die Zahl 
eingesetzt, um den Grenzwert zu berechnen. Wenn nicht konkret gegeben ist und der Funktionsterm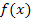 
zugleich 
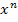und x enthält oder mehrere verschiedene Potenzen von x, wird die Faktorisierung des Zählers sehr schwierig. Das Gleiche gilt für die Polynomdivision (Zähler durch Nenner).
Bei der Delta-x-Methode muss zu Beginn unter anderem der Term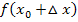 
gebildet und vereinfacht werden. Das ist oft ziemlich aufwändig. Entsprechend muss bei der h-Methode der Term 
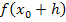berechnet werden, was genauso zeitraubend ist. Eine entsprechende Rechnung bleibt einem bei der 3. Variante allerdings erspart. So hat auch die 3. Variante ihren Vorteil.
Alle drei Varianten haben also ihre Vor- und Nachteile. Es hängt eben von der jeweiligen Aufgabe ab, welche Variante am schnellsten geht. Doch insgesamt ist wohl die h-Methode der beste Weg, die Ableitung mit dem Differenzialquotienten zu berechnen. Sie funktioniert wenigstens immer, egal bei welcher Funktion und egal, ob die Stelle explizit angegeben ist oder nicht. Die Delta- x-Methode klappt natürlich auch immer, bloßschreibt sich 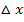nicht so schön wie h. Deshalb ist die h-Methode etwas angenehmer als die Delta- x-Methode, obwohl es sich dabei an sich nicht um einen anderen Rechenweg handelt, sondern nur um eine andere Schreibweise.
Die Berechnung der Ableitung einer Funktion mit dem Differenzialquotienten ist und bleibt aber unabhängig von der gewählten Variante eine langwierige Sache. Erfreulicherweise kann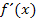 
aber auch viel einfacher gebildet werden.
