Welchen Ansatz bei welchen Aufgaben verwenden
Dann wird der Hilfspunkt H immer näher an den festen Punkt P herangeschoben, bis letztendlich aus der Sekante die Tangente in P wird. Dadurch kann die gesuchte Tangentensteigung aus der Sekantensteigung hergeleitet werden. Je nach gewählter Variante wird allerdings, der Hilfspunkt H unterschiedlich bezeichnet:
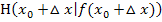bei der 1. Variante, der sogenannten „Delta-x-Methode“
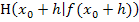bei der 2. Variante, der „h-Methode“
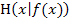bei der 3. Variante
Dadurch ergeben sich die drei unterschiedlichen Ansätze für den Differenzialquotienten, d.h. für die Tangentensteigung an der Stelle 
:
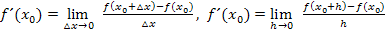und 
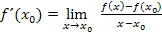
Vorsicht:
Bei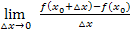 
wird der Abstand 
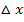der beiden x-Koordinaten von P und H beliebig klein gemacht, also der Grenzwert 
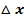gegen Null berechnet. Entsprechend wird bei 
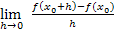der Grenzwert h gegen Null berechnet, weil h dem 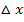aus dem ersten Ansatz entspricht. Man setzt also bei der Delta-x-Methode bzw. bei der h-Methode am Schluss der Rechnung immer 0 für 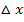bzw. h ein, um den Grenzwert zu berechnen.
Dagegen wird bei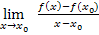 
die x-Koordinate x des Hilfspunktes H direkt an den festen Punkt 
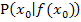, d.h. an die Stelle herangeschoben und daher der Grenzwert x gegen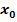 
berechnet. Rechnet man mit dieser Variante des Differenzialquotientens, setzt man also zum Schluss der Rechnung grundsätzlich die für angegebene Zahl für x ein, um den Grenzwert zu berechnen. (Diese Zahl ist natürlich nicht zwangsläufig 0.) Ist für keine konkrete Zahl angegeben, setzt man am Ende der Rechnung entsprechend allgemein für x ein, um den Grenzwert zu berechnen.
In der konkreten Rechnung unterscheiden sich die ersten beiden Formen 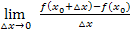und 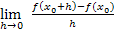kaum voneinander;ob man nun 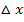oder h schreibt, macht ja keinen großen Unterschied. Allerdings besteht zwischen diesen beiden und der dritten Variante 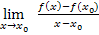ein beträchtlicher Unterschied:Mit der Formel 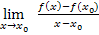lässt es sich nämlich leider oft nicht so gut rechnen. Dennoch arbeiten viele Lehrer gerade auf der FOS in Bayern mit diesem Ansatz.
Wie oben schon erwähnt, lässt es sich mit dem Differenzialquotienten in der Form 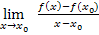vor allem dann nicht gut rechnen, wenn allgemein mit gerechnet werden muss, weil in der Aufgabe keine konkrete Zahl für angegeben ist.
In besonderen Fällen lässt sich die Tangentensteigung an einer bestimmten Stelle mit der Form 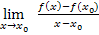des Differenzialquotienten (Variante 3) allerdings schneller berechnen als mit 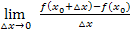bzw. 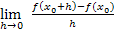. Wenn sich der Zähler des Differenzialquotienten in der Form 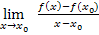leicht faktorisieren lässt, beispielsweise mit einer binomischen Formel, ist diese 3. Variante des Differenzialquotienten zu bevorzugen. Dies ist z.B. dann der Fall, wenn im Funktionsterm nur 
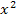, aber kein x vorkommt.
