Variante 3
Für alle, die Probleme mit der Umformung der binomischen Formel haben, hier noch eine kleine Hilfe:
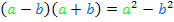
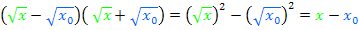
Nun kannst du die folgende Umformung mit Hilfe der binomischen Formel sicher gut nachvollziehen:
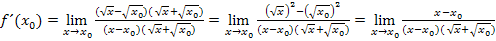
Jetzt erkennst du sicher, was uns das Erweitern zur dritten binomischen Formel gebracht hat. Offensichtlich lässt sich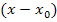 
nun wegkürzen, so dass sich der Grenzwert dann leicht berechnen lässt, da nach dem Kürzen von 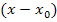der Nenner nicht mehr Null ergibt, wenn man 
für x einsetzt.
Versuche ab hier alleine weiter zu rechnen, ohne vorher auf die folgende Lösung zu schauen! du musst nur 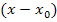kürzen und danach den Grenzwert berechnen, indem du für x einsetzt. Dann fasst du noch soweit möglich zusammen. Los geht´s!
Wenn du richtig gerechnet hast, hast du Folgendes erhalten:
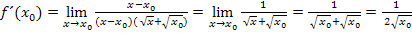
Die Ableitung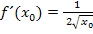 
an der Stelle kennen wir jetzt. Um die Ableitungsfunktion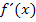 
zu erhalten, muss nur noch rein formal durch x ersetzt werden:
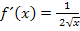
Die Ableitungsfunktion haben wir somit berechnet. Nun sollen aber noch jeweils die maximalen Definitionsmengen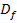 
und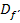 
angegeben und miteinander verglichen werden.
Die Funktion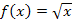 
ist für alle positiven, reellen Zahlen einschließlich Null definiert. (Aus negativen Zahlen kann die Wurzel ja nicht gezogen werden.) Daher gilt für die Definitionsmenge der Funktion:
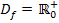
Die Ableitungsfunktion 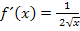ist zwar auch für alle positiven, reellen Zahlen definiert, jedoch nicht für x = 0, denn sonst würde der Nenner Null ergeben. Deshalb gilt für die Definitionsmenge der Ableitungsfunktion:
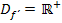
Die Definitionsmenge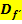 
der Ableitungsfunktion wird übrigens auch als Differenzierbarkeitsbereich bezeichnet. Der Differenzierbarkeitsbereich 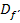und die Definitionsmenge 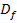der Funktion stimmen in diesem Fall nicht überein. Die Ableitungsfunktion ist an der Stelle x = 0 nicht definiert;die Funktion selbst ist dagegen an dieser Stelle sehr wohl definiert. An der Stelle x = 0 lässt sich die Ableitung 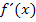also nicht berechnen, obwohl die Funktion selbst dort definiert ist. Man sagt:Die Funktion 
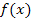ist an der Stelle x = 0 nicht differenzierbar. Das bedeutet, dass an dieser Stelle die Steigung der Funktion nicht berechnet werden kann. Das liegt in diesem Fall daran, dass die Tangente an die Wurzelfunktion 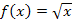bei x = 0 senkrecht verläuft. Ihre Steigung wäre demnach unendlich groß. Betrachte dazu die folgende Abbildung!
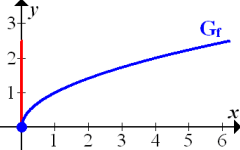
Abb.: Graph der Wurzelfunktion 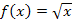mit senkrechter Tangente (rot) im Punkt (0|0)
Damit sind wir mit dieser Aufgabe fertig! Den Trick mit dem Erweitern zur dritten binomischen Formel bei der Berechnung des Differenzialquotienten einer Funktion mit Wurzel solltest du dir gut merken.
