Variante 3
Danach kann der Grenzwert leicht berechnet werden, weil dann der Nenner nicht mehr Null wird, wenn man für x die Zahl 1 einsetzt.
Kürzen des Faktors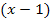 
liefert:
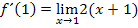
Jetzt muss nur noch für x die Zahl 1 eingesetzt werden.
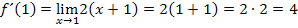
Damit sind wir fertig. Die Funktion hat an der Stelle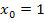 
die Steigung 4.
Und hier gleich noch ein paar weitere Aufgabenbeispiele zur Berechnung des Differenzialquotienten:
3. Bsp.:
Gegeben ist die Funktion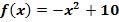 
. Es soll die Steigung der Funktion in den Punkten P(2|f(2)), Q(3|f(3)) und R(4|f(4)) berechnet werden. Ermittle dazu erst die Tangentensteigung in einem beliebigen Kurvenpunkt ( 
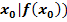und setze danach für 
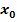die Werte 2, 3 und 4 ein!
Lösung:
Um Zeit zu sparen, wird in dieser Aufgabe nicht dreimal nacheinander der Differenzialquotient für die einzelnen Werte 2, 3 und 4 gebildet. Stattdessen wird der Differenzialquotient nur einmal mit dem allgemeinen Kurvenpunkt (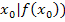 
gebildet. Wir setzen also zu Beginn nicht gleich eine der gegebenen x-Koordinaten in den allgemeinen Ansatz des Differenzialquotienten ein, sondern wir rechnen einfach allgemein mit 
. Dadurch erhalten wir die Ableitung 
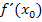. Die gegebenen x-Koordinaten 2, 3 und 4 werden dann erst jeweils für in die Ableitung eingesetzt. Versuch´s doch gleich mal selbst, ohne dir die folgende Lösung anzuschauen! Du musst dabei im Prinzip genauso rechnen, wie im vorherigen Beispiel, allerdings ohne zu Beginn eine konkrete Zahl für einzusetzen. Das Einsetzen der Zahlen 2, 3 und 4 heben wir uns erst einmal für später auf.
Allgemeiner Ansatz für den Differenzialquotienten:
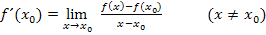
Wir brauchen jetzt die gegebene Funktion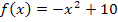 
und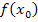 
.
Falls du jetzt nicht weiter weißt:
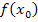erhältst du dadurch, dass du in der Funktionsgleichung statt x einfach schreibst.
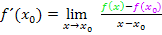
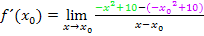
Im Zähler muss erst einmal die Klammer aufgelöst werden. Das Minus vor der Klammer führt dazu, dass sich die Vorzeichen bei allen Zahlen, die vorher in der Klammer standen, umdrehen.
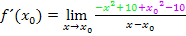
Die Zahlen 10 und -10 im Zähler heben sich gegenseitig auf;sie fallen deshalb weg.
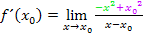
Um den Grenzwert auszurechnen, muss man letztendlich für x einsetzen. In der momentan vorliegenden Form des Differenzialquotienten ist dies aber noch nicht möglich, denn es würde sich dabei Null im Nenner ergeben und das ist ja nicht definiert. Bevor wir für x einsetzen können, muss der Nenner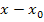 
weggekürzt werden. Damit man den Faktor 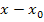herauskürzen kann, muss aber vorweg der Zähler des Differenzialquotientens in ein Produkt umgeformt werden, welches den Faktor 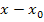enthält. Bloßwie geht das in diesem Fall? Hast du eine Idee?
Bitte erst einmal selbst nachdenken!
