Variante 3

Wie du an diesem Beispiel sehen konntest, ergibt sich bei der Berechnung des Differenzialquotienten manchmal das Problem, dass sich der Nenner nur nach langwieriger Rechnung kürzen lässt. Das Faktorisieren des Zählers ist je nach vorliegender Funktion 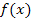schnell geschehen oder dauert sehr lange. Leider kann der Nenner erst dann weggekürzt werden, wenn der Zähler faktorisiert ist.

Anmerkung des Autors:Ich persönlich bevorzuge daher die 2. Methode. Letztendlich musst du jedoch selbst entscheiden, was dir besser liegt.

2. Methode:Verwendung einer Polynomdivision

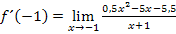
Wir fassen den Bruchstrich des Differenzialquotienten als normales Geteilt-Zeichen auf. Das bedeutet, wir müssen folgende Division durchführen:

(

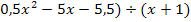
Die Ausdrücke in den Klammern sind jeweils Polynome. Wir müssen deshalb eine Polynomdivision durchführen. Sie geht auf jeden Fall auf. (Wenn sie einmal nicht aufgehen sollte, hast du dich irgendwo verrechnet.)

Die Polynomdivision funktioniert in diesem Beispiel folgendermaßen:

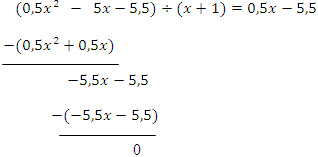
Wir haben dadurch den Bruch 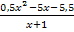ausgerechnet und können nun stattdessen einfach das Ergebnis der Polynomdivision 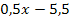schreiben. Du musst allerdings Klammern um dieses Ergebnis setzen, wenn du es hinter den Limes schreibst. Ansonsten wäre es rein formal falsch.

Merke:Immer Klammern um das setzen, worauf sich der limes beziehen soll! (Ausnahmen stellen Ausdrücke dar, die auf einem kompletten Bruchstrich stehen oder unter einer einzigen Wurzel. Ein Bruchstrich wirkt wie eine Klammer, ebenso eine Wurzel. Deshalb kann dann auf die Klammern verzichtet werden.)

Daher gilt:

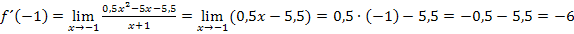
Es ergibt sich natürlich wieder dasselbe Ergebnis, wie schon oben. Die Tangentensteigung 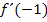ist .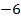

2. Bsp.:

Berechne die Steigung der Funktion 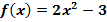im Punkt 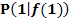mit Hilfe des Differenzialquotienten!

Lösung:

Gesucht ist die Steigung der Funktion 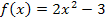an der Stelle 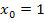, d.h. eigentlich die Steigung der Tangente .

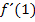Allgemeiner Ansatz:

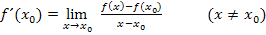
In diesem Beispiel gilt 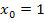. Das setzen wir in den allgemeinen Ansatz ein:

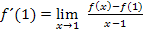
Mit der Funktionsgleichung 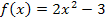ergibt sich:

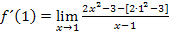
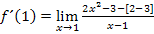
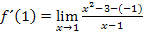
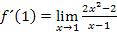
Es bietet sich bei dieser Aufgabe an, im Zähler die Zahl 2 auszuklammern. Danach fällt dir bestimmt etwas auf.

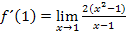
Hast du es gemerkt? Im Zähler kann nun die dritte binomische Formelangewendet werden. Versuche das gleich alleine, bevor du weiter liest!

Mit 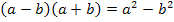ergibt sich:

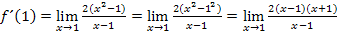
Nun kann der Faktor 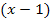weggekürzt werden.

---