Variante 3

Um auf die Einheit der Ableitung zu kommen, musst du nur die Einheit der Funktion durch die Einheit der Variablen teilen. An der Einheit der Ableitung kannst du ihre konkrete Bedeutung meist leichter erkennen. Gibt die Funktion 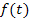beispielsweise einen Weg oder eine Höhe in Metern an und steht t für die Zeit in Sekunden, muss die Ableitung 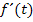die Einheit Meter pro Sekunde, also 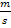, haben. Dass dies die Einheit einer Geschwindigkeit darstellt, ist klar. Deshalb muss die Ableitung in diesem Fall für eine Geschwindigkeit stehen.

Das soll uns hier an Beispielen zur Ableitung, also der Tangentensteigung oder der lokalen Änderungsrate, mit dem Differenzialquotienten reichen. Genaueres zur Ableitungsfunktion f´(x) findest du im Teil Die Ableitungsfunktion f´(x). Wie man die Ableitung f´(x) einer Funktion f(x) wesentlich einfacher als mit dem Differenzialquotienten berechnen kann, wird gezeigt im Teil Einfache Ableitungsregeln. Wie schon weiter oben erwähnt, empfiehlt es sich, ausnahmsweise etwas vorzulernen und das Kapitel mit den (einfachen) Ableitungsregeln schon einmal durchzulesen, auch wenn ihr es in der Schule noch nicht durchgenommen habt. Damit kannst du dein Ergebnis des Differenzialquotientens selbst leicht überprüfen.

---