Variante 3
Die momentane Beschleunigung des Autos nach 3 Sekunden Fahrt beträgt also genau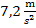 
. Fertig!
Zur anschaulichen Bedeutung der Ableitung in diversen Anwendungsbeispielen
Mache dir zum Abschluss dieses Teils noch einmal klar, was die Ableitung einer bestimmten Funktion anschaulich bedeuten kann. Das hängt ja vom jeweiligen Sachzusammenhang ab. Was bedeutet die Ableitung beispielsweise anschaulich in den folgenden Fällen:
Wenn eine Funktion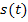 
den zurückgelegten Weg und t die Zeit beschreibt, was gibt dann die Ableitung 
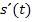an? Richtig, dann ist 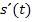die relative Veränderung des Weges pro Zeit, also die momentane Geschwindigkeit zum Zeitpunkt t. Erinnere dich dazu an die physikalische Formel 
.
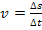Die Momentangeschwindigkeit zum Zeitpunkt t ist daher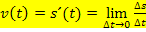 
.
Wenn eine Funktion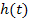 
die Höhe einer Kerze angibt, wobei t für die Zeit steht, die seit dem Entzünden der Kerze vergangen ist, was beschreibt dann die Ableitung 
? Bist du d´rauf gekommen? Die Ableitung entspricht dabei der Abbrenngeschwindigkeit der Kerze.
Ein anderes Anwendungsbeispiel wäre eine Funktion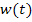 
, welche die Menge des durch eine Pumpe geförderten Wassers beschreibt, wobei t die seit dem Einschalten der Pumpe vergangene Zeit darstellt. Die Ableitung 
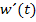entspräche dann der momentanen Pumpleistung zum Zeitpunkt t, also der Menge des gepumpten Wassers pro Zeit zu diesem Zeitpunkt. Je höher die Pumpleistung, desto schneller fließt das Wasser in der Leitung. Daher hängt die Fließgeschwindigkeit des Wassers in der Leitung direkt mit der Pumpleistung oder Förderleistung der Pumpe zusammen. Die Ableitung 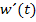gibt hier nicht explizit die Fließgeschwindigkeit des geförderten Wassers an, sondern die Förder- bzw. Pumpleistung der Pumpe an. Doch das ist hier schließlich fast das Selbe.
Wenn eine Funktion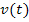 
die Geschwindigkeit zum Zeitpunkt t beschreibt, was entspricht dabei anschaulich die Ableitung 
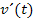? Klar, dann ist 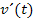die Beschleunigung, die zum Zeitpunkt t wirkt. Denk dabei auch an die Formel 
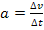, die dir aus der Physik bekannt sein dürfte.
Die momentane Beschleunigung zum Zeitpunkt t ist daher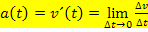 
.
Es gibt noch unzählige ähnlicher Anwendungsaufgaben. Die Ableitung einer Funktion steht also nicht nur für die Tangentensteigung, sondern hat in Anwendungsaufgaben auch immer eine konkrete Bedeutung.
TIPP:Wenn du Schwierigkeiten hast, die Bedeutung der Ableitung in einer bestimmten Anwendungsaufgabe herauszufinden, solltest du die jeweiligen Einheiten in deine Überlegung miteinbeziehen.
