Variante 3
Die durchschnittliche Beschleunigung im Zeitintervall [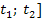 
ist somit nichts anderes als die mittlere Geschwindigkeitsänderung in diesem Zeitabschnitt. In anderen Worten:Als durchschnittliche Beschleunigung bezeichnet man die mittlere Änderungsrate der Geschwindigkeit 
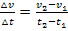. Dies ist der Differenzenquotient der Funktion 
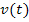. In der nächsten Teilaufgabe wird als konkretes Beispiel die mittlere Beschleunigung für t 
[1;3] berechnet.
Der Differenzenquotient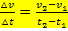 
gibt hier also die mittlere Geschwindigkeitsänderung, d.h. die mittlere Beschleunigung 
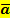im Zeitintervall [ 
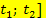an.
Als Momentanbeschleunigung bezeichnet man dagegen die Beschleunigung des Sportwagens zu einem bestimmten Zeitpunkt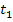 
, also nicht innerhalb eines Zeitintervalls, sondern in einem Moment. (Daher auch die Bezeichnung.) Diese momentane Beschleunigung entspricht der sogenannten momentanen Änderungsrate der Geschwindigkeit. Man erhält sie durch Grenzübergang, indem man die Länge des Zeitintervalls 
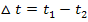gegen Null gehen lässt. Dies entspricht dem Differenzialquotienten der Funktion .
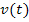Der Differenzialquotient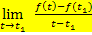 
gibt hier somit die momentane Änderungsrate der Geschwindigkeit, also die momentane Beschleunigung 
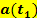zum Zeitpunkt 
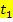an.
In der Lösung von Teilaufgabe 8d.) kannst du sehen, wie die momentane Beschleunigung des Sportwagens nach genau 3 Sekunden berechnet werden kann.
Zu 8c.)
Es soll die mittlere Beschleunigung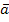 
innerhalb der ersten bis zur dritten Sekunde, also die durchschnittliche Geschwindigkeitsänderung im Vergleich zur dafür benötigten Zeit, berechnet werden.
Dies entspricht dem Differenzenquotienten der Funktion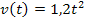 
für t [1;3].
Hier noch einmal die benötigten Daten, die wir schon für die Wertetabelle berechnet haben:
Mittlere Beschleunigung für t [1;3]:
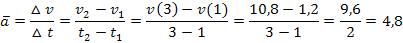
Die mittlere Beschleunigung 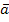innerhalb der ersten bis zur dritten Sekunde beträgt 
.
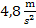zu 8d.)
Wir sollen in dieser Teilaufgabe die momentane Beschleunigung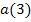 
nach 3 Sekunden Fahrt ermitteln. Dies entspricht dem Differenzialquotienten der Funktion 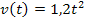zum Zeitpunkt 
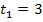. Der Differenzialquotient lässt sich auf folgende Art und Weise schreiben:
Momentane Beschleunigung zum Zeitpunkt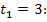 
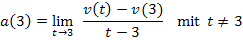
Dafür braucht man 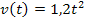und v(3) = 10,8. Eingesetzt ergibt dies:
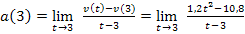
Im Zähler klammern wir den Faktor 1,2 aus. Dadurch ergibt sich in der Klammer ein Term, der sich mit der dritten binomischen Formel umformen lässt.
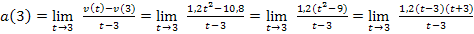
Wie es jetzt weiter geht, ist dir sicherlich klar. Wir kürzen den Faktor t – 3. Dadurch fällt der Nenner weg und der Grenzwert kann ganz leicht durch Einsetzen von 3 für t berechnet werden. Das kannst du bestimmt auch alleine weiterrechnen. Versuch es doch gleich ´mal!
