Variante 3
c.) Berechne die mittlere Beschleunigung des Autos von der ersten bis zur dritten Sekunde.
d.) Welche momentane Beschleunigung wirkt auf das Auto genau 3 Sekunden nach dem Start?
Lösung:
Zu 8a.)
Das Erstellen der Wertetabelle und das Zeichnen des Funktionsgraphen dürfte kein Problem für dich darstellen. Daher keine weitere Erklärung dazu.
Wertetabelle zu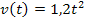 
für 
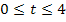mit △t = 0,5
| t in s | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 |
v in  |
0 | 0,3 | 1,2 | 2,7 | 4,8 | 7,5 | 10,8 | 12,25 | 19,2 |
………………………………………………………..
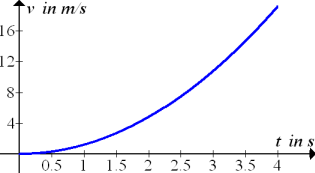
Abb.:Graph der Funktion 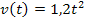für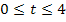
Zu 8b.)
Die Änderung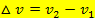 
bezeichnet man als absolute Änderung der Geschwindigkeit. Sie gibt an, wie stark sich die Geschwindigkeit des Autos innerhalb eines bestimmten Zeitintervalls ändert, aber nicht in Bezug auf die dabei vergangene Zeit △t. Die absolute Änderung der Geschwindigkeit hat die gleiche Einheit wie die Geschwindigkeit v, also in diesem Fall die Einheit .
Will man beispielsweise die absolute Geschwindigkeitsänderung von der ersten bis zur dritten Sekunde berechnen, benötigt man die Geschwindigkeit zu Beginn des Zeitintervalls, also zum Zeitpunkt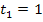 
, und die Geschwindigkeit am Ende des Zeitintervalls, also zum Zeitpunkt 
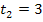. Die zugehörigen Werte der Geschwindigkeit 
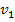und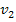 
können entweder mit der Funktionsgleichung 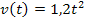berechnet oder in diesem Fall einfach aus der Wertetabelle entnommen werden;da haben wir diese Werte schon berechnet. Es gilt: 
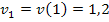und 
.
Absolute Geschwindigkeitsänderung von der ersten bis zur dritten Sekunde:
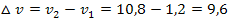
So ändert sich die Geschwindigkeit von der ersten bis zur dritten Sekunde um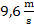 
.
Die mittlere (durchschnittliche) Änderung der Geschwindigkeit erhält man, wenn man die absolute Geschwindigkeitsänderung relativ zur dabei vergangenen Zeit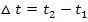 
betrachtet. Man berechnet die mittlere Geschwindigkeitsänderung, indem man die absolute Geschwindigkeitsänderung 
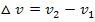durch die bei der Bewegung vergangene Zeit 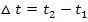dividiert.
Mittlere Geschwindigkeitsänderung:
Die Einheit der mittleren Geschwindigkeitsänderung ist dementsprechend pro Sekunde, also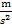 
.
Da das Auto in diesem Beispiel immer schneller wird, sagt man auch umgangssprachlich:„Es beschleunigt.“ Je mehr sich die Geschwindigkeit innerhalb einer bestimmten Zeit ändert, desto größer ist die Beschleunigung. Die Beschleunigung a ist schließlich die relative Veränderung der Geschwindigkeit im Vergleich zur Zeit.
