Variante 3
Nun aber endlich die Berechnung der Tangentensteigung zu 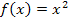 im Punkt
im Punkt 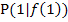 aus unserem Einführungsbeispiel.
aus unserem Einführungsbeispiel.
Allgemeiner Ansatz für die Tangentensteigung im Punkt 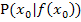 :
:
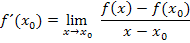
Ansatz für die Tangentensteigung im Punkt 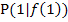 :
:
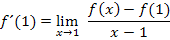
Achtung:Ausschließlich für  wird die x-Koordinate 1 des gegebenen Punktes
wird die x-Koordinate 1 des gegebenen Punktes 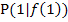 in den allgemeinen Ansatz des Differenzialquotienten eingesetzt, nicht aber für x! Für x darf hierbei nichts eingesetzt werden!
in den allgemeinen Ansatz des Differenzialquotienten eingesetzt, nicht aber für x! Für x darf hierbei nichts eingesetzt werden!
Nun bilden wir noch 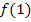 . Dazu muss in die gegebene Funktionsgleichung
. Dazu muss in die gegebene Funktionsgleichung 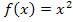 für x die Zahl 1 eingesetzt werden:
für x die Zahl 1 eingesetzt werden:
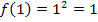
Damit ergibt sich für den Differenzialquotienten an der Stelle 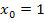 :
:
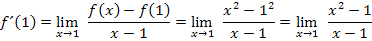
So und nun? Um den Grenzwert zu berechnen, muss hier letztendlich x beliebig nah gegen 1 gehen. Eigentlich heißt das, dass man für x die Zahl 1 einsetzen muss. Doch dann wird der Nenner gleich Null und das ist nicht definiert. Was also tun? Hast du eine Idee? (Tipp:Schau dir doch mal den Zähler genau an. Was fällt dir daran auf?)
Hast du erkannt, dass der Term im Zähler mit der dritten binomischen Formel in ein Produkt umwandeln lässt?
Zur Erinnerung hier die dritte binomische Formel: 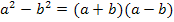
Wir formen nun den Zähler mit Hilfe der dritten binomischen Formel um. Das ergibt:
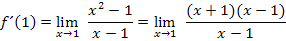
Jetzt liegt im Zähler ein Produkt vor und wir dürfen kürzen.
Durch Kürzen des Faktors 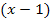 erhält man:
erhält man:
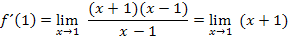
Jetzt kann für x die Zahl 1 eingesetzt werden, ohne dass der Nenner Null wird. Wir können nun den Grenzwert leicht ausrechnen. (Einfach für x die Zahl 1 einsetzen.
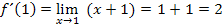
Die Tangente im Punkt 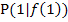 an die Funktion
an die Funktion 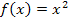 hat somit die Steigung 2.
hat somit die Steigung 2.
Halten wir nun kurz die einzelnen Schritte bei der Berechnung der Tangentensteigung in einem bestimmten Kurvenpunkt 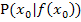 mit dem Differenzialquotienten fest.
mit dem Differenzialquotienten fest.
Geg.: 
Anleitung zur Berechnung der Tangentensteigung Ansatz: · x-Koordinate des gegebenen Punktes P ausschließlich für · Zähler des Ausdrucks in ein Produkt umwandeln (faktorisieren) durch evtl. Ausklammern oder auch Anwendung einer binomischen Formel, anschließend den Faktor Oder alternativ dazu:Den vorliegenden Bruch mit Hilfe einer Polynomdivision ausdividieren; dabei einfach Zähler durch Nenner teilen (keines der Vorzeichen im Nenner umdrehen!) · Grenzwert berechnen, d.h. für x die gegebene Zahl Das Ergebnis des Grenzwertes ist eine konkrete Zahl, welche die Steigung der Funktion / der Tangente im Kurvenpunkt |
Schauen wir uns doch gleich ein paar typische Beispielaufgaben zur Berechnung des Differenzialquotienten an!

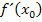 im Punkt
im Punkt 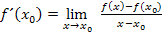
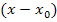 aus dem Nenner wegkürzen
aus dem Nenner wegkürzen