Variante 3
Tangentensteigung im Punkt A: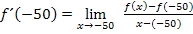 
( 
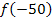müssen wir nicht mehr berechnen, da dies ja der y-Koordinate des Punktes A(-50|0) entspricht. Deshalb gilt: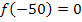 
Einsetzen der Funktionsgleichung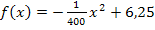 
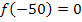und in unseren Ansatz des Differenzialquotienten ergibt:
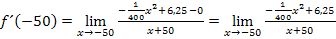
Nun müssen wir den Grenzwert aber noch ausrechnen. In der momentan vorliegenden Form kann für x der Wert -50 noch nicht eingesetzt werden, da der Nenner gleich Null werden würde. Um den Grenzwert zu berechnen, müssen wir aber für x genau den Wert -50 einsetzen können. Deshalb muss vorher derart umgeformt werden, dass sich x + 50 wegkürzen lässt. Erst danach kann der Grenzwert durch Einsetzen von x = -50 berechnet werden. Also, los geht´s mit den Umformungen!
Im Zähler klammern wir erst einmal den Faktor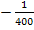 
aus. Warum? Das wird dir sicher gleich von selbst klar.
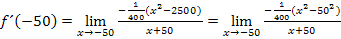
Hast du erkannt, was nun im Zähler vorliegt?
Richtig! Eine binomische Formel! Und welche ist es? Klar, schon wieder die dritte binomische Formel, wie schon in den Beispielen 2 und 3!
Nach dem Ausklammern des Bruchs erkennt man doch wesentlich leichter, dass im Zähler die dritte binomische Formel vorliegt. Durch die Anwendung der binomischen Formel kann man den Zähler dann so umformen, dass sich x + 50 kürzen und anschließend der Grenzwert berechnen lässt. (Aus genau diesem Grund wurde vorher ausgeklammert.)
Zur Erinnerung: Dritte binomische Formel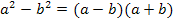 
Damit ergibt sich:
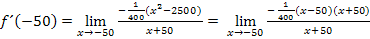
Nun können wir endlich den Faktor x + 50 wegkürzen.
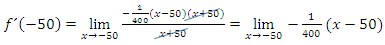
Jetzt kann der Grenzwert leicht berechnet werden:Man braucht nur für x den Wert -50 einsetzen. Es gibt ja nun keinen Nenner mehr, der Null ergeben könnte. Also gibt es auch kein Problem mehr bei der Berechnung des Grenzwertes.
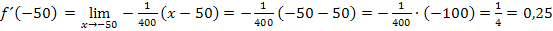
Wie schon erwartet, ergibt sich für die Tangentensteigung im Punkt A der Wert 0,25.
Man kann diesen Wert übrigens auch in Prozent angeben. Dazu muss man nur das Komma um zwei Stellen nach rechts verschieben. Die Tangente hat somit in A eine Steigung von 25%.
Mit der Formel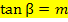 
lässt sich auch der Neigungswinkel 
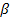der Tangente gegenüber der Horizontalen berechnen, wobei m für die Steigung der Tangente an der Stelle 
steht. Es gilt daher: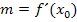 
Zu der Steigung m = 0,25 bzw. m = 25% gehört ein Neigungswinkel 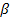von ungefähr 14,04°. Das kannst du selbst folgendermaßen nachrechnen:
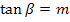
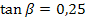
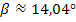
Mit dem Taschenrechner erhältst du mit der Tastenfolge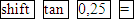 
das oben gezeigte Ergebnis von ungefähr 14,04° für 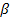. (Achtung:der Taschenrechner muss auf den mode DEG bzw. D für degree/ Grad eingestellt sein!)
Dies ist jetzt der Winkel, unter dem der Brückenbogen die Horizontale im Punkt A schneidet. Vergleiche dazu die folgende Abbildung!
