Variante 3
Zu Beginn des Kapitels wurde bereits erklärt, dass man die Tangentensteigung in einem bestimmten Punkt – in dieser Aufgabe A genannt – erhält, indem man sich einen Hilfspunkt H vorstellt und diesen immer näher an den festen Punkt A heranschiebt. So kann aus der Sekantensteigung, also dem Differenzenquotienten, die Tangentensteigung, also der Differenzialquotient, hergeleitet werden. Die Sekantensteigung stellt also die mittlere (durchschnittliche) Höhenänderung zwischen zwei Punkten dar;die Tangentensteigung die lokale Höhenänderung an einem Punkt. Durch Grenzübergang erhalten wir aus der Sekantensteigung letztendlich die Tangentensteigung, also die lokale Änderungsrate der Höhe, wie in der Aufgabe verlangt. (Mit „Grenzübergang“ ist gemeint, dass man den Grenzwert des Differenzialquotienten berechnen soll.)
Nun berechnen wir erst einmal, wie verlangt, die durchschnittlichen Sekantensteigungen (mittleren Änderungsraten der Höhe) zwischen A und jeweils einem der Hilfspunkte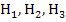 
und 
.
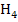Wir beginnen mit A(-50| 0) und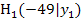 
, da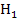 
am weitesten von A entfernt ist. Dazu brauchen wir noch die y-Koordinate von 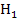. Wir erhalten sie durch Einsetzen der x-Koordinate von 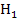in die Funktionsgleichung der Parabel 
.
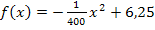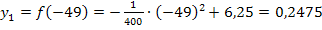
Der Punkt 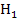lautet also 
.
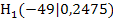Jetzt bilden wir den Differenzenquotienten, um die mittlere Höhenänderung zwischen A und 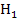, d.h. die Sekantensteigung, zu berechnen: A(-50| 0) und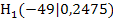
Sekantensteigung zwischen A und :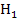 
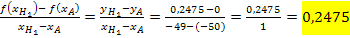
Entsprechend gehen wir nun mit den Punkten A und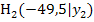 
vor.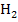 
liegt schon etwas näher an A als 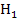. Die x-Koordinaten von A und 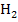unterscheiden sich nur noch um 0,5. Dagegen war die x-Koordinate von 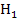noch um 1 größer als die x-Koordinate von A. Wir brauchen nun die y-Koordinate von .
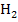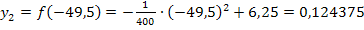
Der Punkt 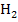lautet also 
.
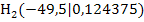Jetzt bilden wir den Differenzenquotienten, um die mittlere Höhenänderung zwischen A und 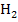, d.h. die Sekantensteigung, zu berechnen: A(-50;0) und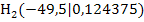
Sekantensteigung zwischen A und :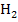 
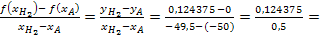
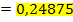
Weiter geht´s mit den Punkten A und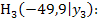 
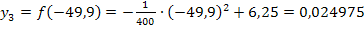
Der Punkt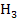 
lautet also 
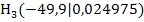. Er liegt noch näher an A als 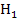und 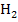. Die x-Koordinaten von A und 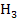unterscheiden sich nur um 0,1.
Jetzt bilden wir den Differenzenquotienten, um die mittlere Höhenänderung zwischen A und 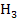, d.h. die Sekantensteigung, zu berechnen: A(-50;0) und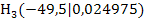 
Sekantensteigung zwischen A und :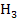 
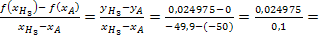
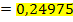
Und noch einmal mit dem letzten Punkt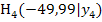 
:
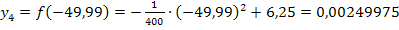
Der Punkt 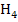lautet also 
.
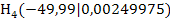