Variante 3
Hier noch ein paar zusätzliche Informationen:
Die mittlere Änderungsrate (Sekantensteigung) wird oft auch in Prozent angegeben. Dazu muss nur das Komma um zwei Stellen nach rechts verschoben werden. (Prozent kommt schließlich von „pro centum“, also von „auf Hundert“ gesehen.)
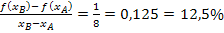
Eine Steigung von 12,5 % bedeutet, dass man auf 100 m horizontaler Strecke 12,5 m an Höhe gewinnt.
Eine Steigung von 100% würde dementsprechend bedeuten, dass man auf 100 m horizontaler Strecke 100 m an Höhe gewinnt, d.h. 100% Steigung entspricht einem 45° Winkel gegenüber der Horizontalen und nicht 90°, was nämlich viele Leute glauben. Der Steigungswinkel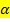 
lässt sich mit der Formel 
berechnen, wobei m für die Steigung der Geraden steht.
Zu der Steigung m = 0,125 bzw. m = 12,5% gehört ein Steigungswinkel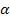 
von ungefähr 7,1°. Das kannst du folgendermaßen nachrechnen:
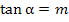
Mit dem Taschenrechner erhältst du mit der Tastenfolge 
das oben gezeigte Ergebnis von ungefähr 7,1° für .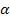
Es soll betont werden, dass es sich bei diesem Winkel nur um den Winkel zwischen der Sekanten AB und der Horizontalen handelt und nicht um den Winkel, unter dem die Brücke den Boden im Punkt A schneidet. Wir haben ja mit dem Wert m = 0,125 gerechnet und dies ist nur die durchschnittliche Steigung zwischen den Punkten A und B, aber nicht die Steigung im Punkt A. Im Punkt A verläuft die Parabel wesentlich steiler, was zu einem wesentlich größeren Winkel zwischen Brücke und Boden führt. Um den Winkel zwischen Brücke und Boden im Punkt A zu berechnen, bräuchten wir zuerst die Steigung der Brücke genau im Punkt A, also die Tangentensteigung im Punkt A. Dies kommt aber erst in der nächsten Teilaufgabe.
Abb.: Graph der Parabel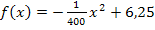 
mit x 
[-50;50] mit Sekante AB, Neigungswinkel 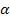der Sekante und Tangente im Punkt A.
Zu 7c.)
In dieser Teilaufgabe soll zuerst jeweils die mittlere Änderungsrate der Höhe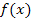 
, also die durchschnittliche Steigung der Brücke, zwischen den Punkten A und 
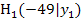, den Punkten A und 
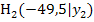, den Punkten A und 
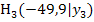sowie Punkten A und 
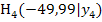berechnet werden. Die Punkte 
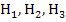und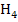 
sind Beispiele für den am Anfang des Kapitels erwähnten Hilfspunkt H.
