Variante 3
Gefragt ist also, wie stark sich die Höhe des Fußgängers im Vergleich zur horizontal zurückgelegten Strecke ändert, wenn er von einem bestimmten Punkt zu einem anderen über die Brücke geht. Dies entspricht der durchschnittlichen Steigung der Brücke zwischen diesen zwei Punkten. Und das ist wiederum nichts anderes als die Sekantensteigung. Die mittlere Höhenänderung ist wesentlich aussagekräftiger als nur die absolute Höhenänderung. So lässt sich ausschließlich von der mittleren Höhenänderung auf die Steilheit der Brücke schließen, nicht aber von der absoluten Höhenänderung. Aus der absoluten Höhenänderung von 6,25 m geht offensichtlich nicht hervor, wie steil die Brücke ist. Würde man beispielsweise auf nur 1 m horizontaler Strecke nach vorne schon 6,25 m an Höhe gewinnen, wäre dies viel steiler, als wenn man auf 10 m horizontaler Strecke 6,25 m an Höhe gewinnen würde. Vergleiche dazu auch die folgenden Skizzen!
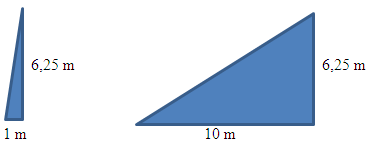
Um eine Aussage betreffs der mittleren Steigung der Brücke zwischen zwei bestimmten Punkten machen zu können, muss man die absolute Höhenänderung im Vergleich zur dabei zurückgelegten horizontalen Strecke betrachten.
Daher gibt man die mittlere (durchschnittliche) Höhenänderung an, welche im Allgemeinen auch als mittlere Änderungsrate von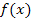 
bezeichnet wird.
Um die mittlere Höhenänderung zu erhalten, muss man die absolute Höhenänderung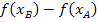 
zwischen den Punkten A und B in Bezug setzen zur horizontal zurückgelegten Strecke 
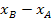. Genauer gesagt:Es muss die absolute Höhenänderung 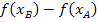durch die Länge der horizontal zurückgelegten Strecke 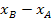dividiert werden, um die mittlere Höhenänderung zu bekommen.
Mittlere Höhenänderung (mittlere Änderungsrate):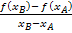 
Du erkennst sicher, dass es sich hierbei um die Formel für die Steigung einer Geraden durch die Punkte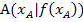 
und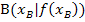 
handelt. Da die Gerade AB Sekante der Funktion 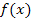ist, stellt die mittlere Höhenänderung nichts anderes als die Sekantensteigung dar. Es handelt sich dabei bekanntlich um den Differenzenquotienten.
Nun müssen wir nur noch die Koordinaten der Punkte A(-50|0) und B(0|6,25) in die Formel für die mittlere Höhenänderung einsetzen. So ergibt sich:
Mittlere Höhenänderung (mittlere Änderungsrate):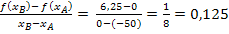 
Die Teilaufgabe 7b.) ist damit gelöst.
