Variante 3
Damit wird die Steigung einer Geraden, die durch zwei Punkte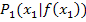 
und 
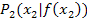festgelegt ist, berechnet. Da es sich bei den beiden Punkten um Kurvenpunkte der Funktion f(x) handelt, ist die Gerade durch 
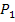und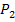 
eine Sekante der Funktion f(x) und somit beschreibt die mittlere Änderungsrate nichts anderes als die Sekantensteigung, also den Differenzenquotienten. Wir haben den Differenzenquotienten bisher immer in der Form 
geschrieben. Das sieht natürlich etwas anders aus als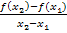 
. Doch wurde bereits oben erwähnt, dass es die alternative Schreibweise 
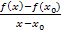gibt. Dies ähnelt 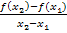schon deutlich mehr. Bitte lass dich nicht durch die verschiedenen Schreibweisen verwirren;letztendlich wird durch jede Form des Differenzenquotienten nichts anderes als die Sekantensteigung 
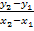bzw.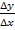 
beschrieben.
Die mittlere Änderungsrate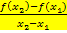 
ist also der Differenzenquotient und gibt die Steigung der Sekante durch die Kurvenpunkte 
und 
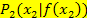an.
Nun zurück zu unserer Aufgabe:
Es soll die mittlere Wertänderung der Aktie zwischen 9 und 11 Uhr, sowie zwischen 10 und 15 Uhr berechnet werden.
Hier ist noch einmal die Tabelle von oben:
| x in Std. | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Wert f(x) in € | 50 | 98 | 182 | 198 | 169 | 146 | 139 | 172 | 152 |
Wir beginnen mit der Berechnung der mittleren Wertänderung zwischen 9 und 11 Uhr. Die nötigen Daten entnehmen wir wieder der Tabelle.
Uhrzeit:
Zugehörige x-Koordinate: Zugehöriger Funktionswert (Wert der Aktie in €)
9 Uhr: x = 1 f(1) = 98
11 Uhr: x = 3 f(3) = 198
Mittlere Wertänderung (in € pro Stunde) zwischen 9 und 11 Uhr:
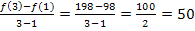
Durchschnittlich nimmt in diesem Zeitraum der Wert der Aktie somit um 50 € pro Stunde zu.
Nun zur Berechnung der mittleren Wertänderung zwischen 10 und 15 Uhr. Die nötigen Daten entnehmen wir wieder der Tabelle.
Uhrzeit: Zugehörige x-Koordinate: Zugehöriger Funktionswert (Wert der Aktie in €)
10 Uhr: x = 2 f(2) = 182
15 Uhr: x = 7 f(7) = 172
Mittlere Wertänderung (in € pro Stunde) zwischen 10 und 15 Uhr:
Die mittlere Wertänderung bzw. die mittlere Änderungsrate des Aktienwerts ist negativ, da der Wert der Aktie in diesem Zeitraum sinkt. Durchschnittlich nimmt in diesem Zeitraum der Wert der Aktie somit um 2 € pro Stunde ab. Anschaulich kannst du dir dies als Steigung der Geraden durch die Punkte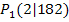 
und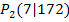 
vorstellen. Die mittlere (durchschnittliche) Änderungsrate entspricht schließlich dem Differenzenquotienten, also anschaulich der Sekantensteigung.
| Fassen wir noch einmal alles, was du an diesem Beispiel lernen solltest, zusammen:
Der Differenzenquotient beschreibt die mittlere (durchschnittliche) Änderungsrate innerhalb eines Intervalls von |
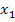bis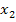 
. Darunter versteht man die Veränderung des Funktionswertes 
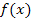bzw. y relativ zur Änderung von x. Die mittlere Änderungsrate kann auch als 
.
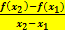