Variante 3
Wir beginnen mit der Berechnung der absoluten Wertänderung von 9 bis 11 Uhr. Dazu müssen wir uns Folgendes überlegen:Die Börse öffnet um 8 Uhr. Von 8 bis 9 Uhr ist 1 Stunde vergangen und von 8 bis 11 Uhr sind logischerweise 3 Stunden vergangen. Da x die Zeit in Stunden seit Öffnung der Börse ist, gehört zur Uhrzeit 9 Uhr die x-Koordinate x = 1 und entsprechend zu 11 Uhr die Koordinate x = 3.
Zur Berechnung der absoluten Wertänderung benötigen wir natürlich den jeweiligen Wert der Aktie um 9 Uhr und um 11 Uhr. Das sind die Funktionswerte zu x = 1 und x = 3, also f(1) und f(3), da f(x) hier den Wert der Aktie nach x Stunden seit Öffnung der Börse angibt. Wir entnehmen diese Werte der bereits oben gezeigten Tabelle. Hier ist sie noch einmal:
| x in Std. | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Wert f(x) in € | 50 | 98 | 182 | 198 | 169 | 146 | 139 | 172 | 152 |
Uhrzeit:
Zugehörige x-Koordinate: Zugehöriger Funktionswert (Wert der Aktie in €)
9 Uhr: x = 1 f(1) = 98
11 Uhr: x = 3 f(3) = 198
Absolute Wertänderung (in €) zwischen 9 und 11 Uhr: f(3) – f(1) = 198 – 98 = 100
Der Wert der Aktie steigt von 9 bis 11 Uhr um 100 €.
Entsprechend gehen wir bei der absoluten Wertänderung von 10 bis 15 Uhr vor. Du musst hier jedoch beachten, dass in diesem Zeitraum der Wert der Aktie abnimmt. Das wird durch ein negatives Vorzeichen bei der Wertänderung ausgedrückt. Du rechnest also für die absolute Wertänderung immer den Wert zum späteren Zeitpunkt minus den Wert zum früheren Zeitpunkt. Mathematisch ausgedrückt:
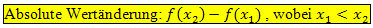
Uhrzeit: Zugehörige x-Koordinate: Zugehöriger Funktionswert (Wert der Aktie in €)
10 Uhr: x = 2 f(2) = 182
15 Uhr: x = 7 f(7) = 172
Absolute Wertänderung (in €) zwischen 10 und 15 Uhr: f(7) – f(2) = 172 – 182 = – 10
Der Wert der Aktie sinkt von 10 bis 15 Uhr um 10 €.
Zu 6b.)
Hier ist nach der mittleren Wertänderung der Aktie, also nach der mittleren Änderungsrate des Aktienwerts gefragt. Im Unterschied zur absoluten Wertänderung bezieht sich die mittlere Wertänderung nicht nur auf die Änderung des Werts in €, sondern auch auf die Zeitspanne, in der dies passiert. Steigt der Wert beispielsweise innerhalb von 1 Stunde um 100 €, ist dies ein wesentlich stärkerer Anstieg des Werts, als wenn dies nur innerhalb von einem Tag geschehen würde. Die mittlere Änderungsrate beschreibt somit den durchschnittlichen Anstieg bzw. Abfall des Funktionswertes innerhalb einer bestimmten Zeitspanne.
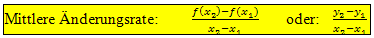
Diese Formeln dürften dir bekannt vorkommen. Richtig!
