Variante 3
Dafür ist diese Variante des Differenzialquotienten an sich nicht geeignet. (Auch bei Funktionen mit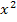 
und x lässt sich 
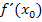mit unbekanntem 
und somit auch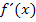 
mit dem Ansatz 
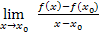berechnen, aber es wird wirklich schwierig. Wesentlich einfacher geht die Berechnung von 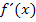mit dem Differenzialquotienten dann zum Beispiel mit der h-Methode.) Warum der Ansatz 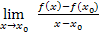des Differenzialquotienten nicht gut geeignet ist, die Ableitungsfunktion 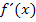bei Funktionen mit 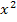und x zu berechnen, kannst du bei Sehr schwieriges Beispiel zum Differenzialquotienten mit Variante 3 sehen. Dort wird vorgeführt, wie die Berechnung von 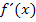mit dem Ansatz 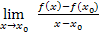bei einer Funktion mit 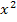und x geht. Bitte nicht erschrecken, ab der Faktorisierung bzw. ab der Polynomdivision wird es ziemlich kompliziert. (Du musst das aber wirklich nur dann selbst können, wenn ihr in der Schule eine ähnliche Aufgabe gemacht habt.)
In den nächsten Beispielen wollen wir uns mit Anwendungsaufgaben des Differenzen- und des Differenzialquotienten beschäftigen. Für Schüler einer 11. Klasse des G8 ist dies besonders wichtig. Die Begriffe Differenzen- und Differenzialquotient lassen sich ja anschaulich nicht nur als Sekanten- und Tangentensteigung deuten, sondern auch als „mittlere Änderungsrate“ und „lokale Änderungsrate“. Was die Begriffe „mittlere Änderungsrate“ und „lokale Änderungsrate“ genau bedeuten, wird an Hand der folgenden Beispiele herausgearbeitet.
6. Bsp.:Wertentwicklung einer Aktie
Der folgende Graph zeigt die Wertentwicklung einer Aktie seit Öffnung der Börse um 8 Uhr bis zum Schluss der Börse um 16 Uhr. x ist die Zeit in Stunden seit Öffnung der Börse.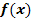 
ist der Wert der Aktie in €.
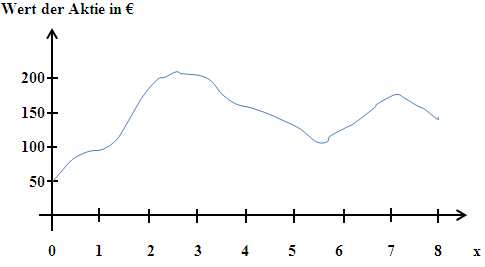
In der folgenden Tabelle kannst du den Wert der Aktie jeweils zur vollen Stunde ablesen:
| x in Std. | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Wert f(x) in € |
50 |
98 |
182 |
198 |
169 |
146 |
139 |
172 |
152 |
a.) Berechne die absolute Wertänderung in € zwischen 9 und 11 Uhr, sowie zwischen 10 und 15 Uhr!
b.) Die mittlere Wertänderung erhält man, indem man die absolute Wertänderung durch die vergangene Zeit dividiert, d.h. die Wertänderung im Verhältnis zur Zeit angibt. Berechne die mittlere Wertänderung zwischen 9 und 11 Uhr sowie zwischen 10 und 15 Uhr!
Lösung:
Zu 6a.)
Die absolute Wertänderung der Aktie gibt an, um wie viel € der Wert der Aktie innerhalb eines bestimmten Zeitraums gestiegen bzw. gesunken ist, um wie viel sie also tatsächlich teurer bzw. billiger geworden ist.
