Variante 3
Das ist an sich egal, denn dadurch dreht sich jeweils bei einem dieser Ausdrücke die Reihenfolge um und dann kann man kürzen. Wir entscheiden uns hier dazu, im Zähler -1 auszuklammern. (Wenn dir der Trick mit dem -1 Ausklammern, um die Reihenfolge bei einer Differenz umzudrehen, nicht bekannt ist, lies bitte die Erklärungen bei Ausklammern.) Durch das Ausklammern von -1 dreht sich nämlich bei einer Differenz immer letztendlich die Reihenfolge um: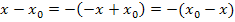 
Ausklammern von -1 im Zähler ergibt:
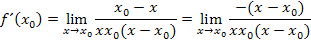
Jetzt kann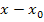 
weggekürzt und der Grenzwert berechnet werden.
Kürzen von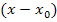 
ergibt:
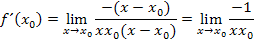
Berechnung des Grenzwertes durch Einsetzen von 
für x:
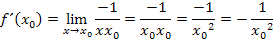
Die Ableitung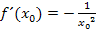 
an der Stelle kennen wir jetzt. Um die Ableitungsfunktion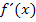 
zu erhalten, muss nur noch rein formal durch x ersetzt werden:
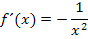
Das ist also die gesuchte Ableitungsfunktion 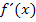der Funktion 
.
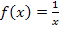Zu 5b.)
Es soll die Gleichung der Tangente im Kurvenpunkt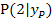 
an die Funktion 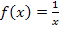berechnet werden. Da eine Tangente eine Gerade ist, gilt für sie auch die allgemeine Geradengleichung y = mx + t, mit der Steigung m und dem y-Achsenabschnitt t.
Als erstes berechnen wir die y-Koordinate des Punktes P. (Wir brauchen sie später bei der Berechnung des y-Achsenabschnitts t.) Weil P ein Punkt des Graphen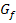 
ist, erhalten wir seine y-Koordinate, indem wir die x-Koordinate von P in die Funktionsgleichung 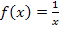einsetzen:
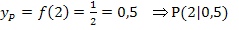
Als nächstes müssen wir die Steigung m der Tangente im Punkt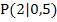 
ermitteln. Die Tangentensteigung erhalten wir durch Einsetzen von x = 2 in die Ableitungsfunktion 
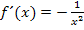. Es gilt somit für die Tangentensteigung:
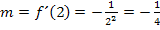
Den y-Achsenabschnitt t erhält man, wenn man die Koordinaten des Punktes 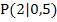für x bzw. y und den soeben berechneten Wert für m einsetzt und nach t auflöst.
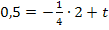
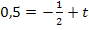
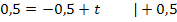
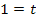
Die Gleichung der Tangente im Punkt P lautet daher: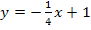 
Fertig!
Bisher wurden keine Beispiele mit Funktionen gezeigt, die gleichzeitig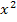 
und x enthalten, aber nicht gegeben ist, also wo mit dem Ansatz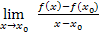 
zum Beispiel die Ableitungsfunktion 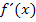gebildet werden muss. Wie schon weiter oben erwähnt, sind solche Berechnungen echt extrem unangenehm, weil sehr schwer. Nur in sehr seltenen Fällen wird ein(e) Lehrer(in) von dir verlangen, dass du mit Hilfe dieser Variante des Differenzialquotienten auch die Ableitungsfunktion 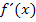berechnen sollst, obwohl die Funktionsgleichung nicht nur 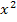sondern auch x enthält.
