Die h-Methode
Um mit Hilfe von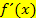 
die Steigung von 
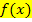in einem bestimmten Kurvenpunkt 
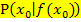zu berechnen, muss dann bloßnoch die gegebene x-Koordinate 
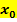des Kurvenpunktes in die Ableitungsfunktion eingesetzt werden und schon hat man die Steigung 
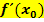der Funktion 
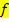in diesem Kurvenpunkt. Das Berechnen der Ableitung 
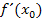an einer bestimmten Stelle 
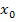nennt man lokales Differenzieren.
Wenn wir einen Weg finden, wie wir die Ableitungsfunktion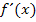 
schnell und einfach ermitteln könnten, also auch ohne h-Methode, wäre es ganz einfach, die Tangentensteigung bzw. die Steigung einer Kurve zu berechnen. Gerade die Ableitungsfunktion 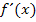wird im Weiteren noch extrem wichtig werden, doch mit ihr beschäftigen wir uns erst eingehender im gesonderten Teil Die Ableitungsfunktionf´(x).
Im Folgenden werden erst noch einige etwas schwierigere Beispiele für die Ermittlung von 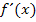mit der h-Methode vorgestellt. Es geht dabei nicht ohne kleine algebraische Tricks. Ganz ohne Hilfe kommt man nur schwer darauf. Daher sollst du diese Tricks hier einmal gezeigt bekommen.
4. Bsp.:
Berechne die Ableitungsfunktion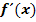 
der Funktion 
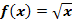mit der h-Methode! Ermittle sodann die maximale Definitionsmenge 
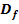der Funktion 
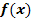und die maximale Definitionsmenge 
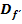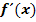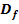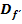der Ableitungsfunktion ! Was fällt dir beim Vergleich von und auf?
Lösung:
Gegeben: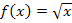 
Gesucht: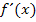
Wir gehen aus vom allgemeinen Ansatz der h-Methode für die Ableitung 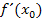einer Funktion 
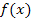an der Stelle 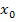. Er lautet:
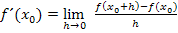
Wir sollen in dieser Aufgabe die Ableitungsfunktion 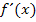ermitteln, also nicht die Ableitung 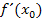einer Funktion 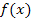an einer bestimmten Stelle 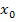, sondern an einer beliebigen Stelle x innerhalb der Definitionsmenge. Dies stellt jedoch kein Problem dar. Man muss nur rein formal 
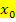durch x ersetzen. Ob man das gleich zu Beginn oder erst am Ende der Rechnung macht, ist egal. Wir rechnen hier die gesamte h-Methode mit 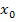durch und ersetzen erst am Schluss 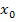durch x.
Nun müssen wir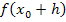 
und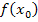 
mit unserer Funktion 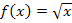bilden, weil diese Ausdrücke im Zähler des Differenzenquotienten benötigt werden. 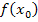zu bilden ist ja nicht schwer;du schreibst einfach statt x in der Funktionsgleichung 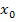. Es gilt daher:
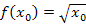
Wie bildet man aber 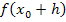? Auch gar nicht so schlimm:Du setzt einfach für x den Ausdruck 
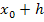in unsere Funktionsgleichung 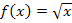ein. So erhältst du:
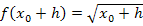
Wenn du das in den allgemeinen Ansatz der h-Methode einsetzt, bekommst du:
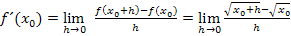
Jetzt müsste man eigentlich h herauskürzen, um den Grenzwert zu berechnen. So lange h im Nenner steht, kann man für h nicht Null einsetzen, was man aber letztendlich bei der Berechnung des Grenzwertes machen muss.
