Die h-Methode
Bald werden wir nämlich einen wesentlich einfacheren Weg kennenlernen. Mit Hilfe der sogenannten Ableitungsregeln lässt sich die Ableitung einer Funktion nämlich meist ganz schnell im Kopf, also ohne viele Zwischenschritte, ermitteln. (Ausführlichere Erläuterungen findest du im Kapitel Einfache Ableitungsregeln.) Es ist hier geschickt, bald etwas vorzulernen. Die Ableitungsregeln sind nämlich sehr leicht zu lernen und man kann damit sein Ergebnis der Ableitung, welches man mit der h-Methode berechnet hat, selbst schnell kontrollieren. Am besten ist es, wenn du dir jetzt gleich mit Hilfe der folgenden Beispiele die h-Methode gut aneignest und dann aber schon das nächste Kapitel Einfache Ableitungsregelndurchliest, auch wenn ihr das in der Schule noch nicht besprochen habt. Die h-Methode ist sehr aufwändig und es schleichen sich bei vielen Schülern rasch Fehler ein. Daher ist es für dich sicher von Vorteil, wenn du bald lernst, dein eigenes Ergebnis der h-Methode mit Hilfe der Ableitungsregeln zu überprüfen. Doch nun erst ´mal wieder zurück zur h-Methode.
Halten wir noch einmal die einzelnen Schritte fest, die du machen musst, um die Tangentensteigung, d.h. die Ableitung 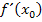 einer Funktion
einer Funktion 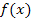 an einer bestimmten Stelle
an einer bestimmten Stelle 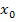 , mit der h-Methode zu berechnen.
, mit der h-Methode zu berechnen.
Geg.: 
Anleitung zur Berechnung der Tangentensteigung im Punkt Ansatz: · Für · Zähler des Ausdrucks so weit möglich vereinfachen, d.h. Klammern auflösen, evtl. dabei eine binomische Formelanwenden und zusammenfassen (Es muss im Zähler alles wegfallen, was kein h enthält! Wenn das nicht der Fall ist, hast du dich verrechnet.) · Im Zähler h ausklammern · Mit h kürzen · Grenzwert berechnen, indem du für h die Zahl Null einsetzt Das Ergebnis des Grenzwertes ist eine konkrete Zahl, welche die Steigung der Funktion bzw. der Tangente im Kurvenpunkt |
Nun folgen einige konkrete Beispiele für die h-Methode. Im 1. bis 5. Beispiel wird jeweils die h-Methode an einigen etwas schwierigeren Beispielen vorgeführt. Ab dem 6. Bsp. kommen die besonders für G8 Schüler extrem wichtigen Anwendungsaufgaben, an Hand derer auch die Begriffe der „mittleren Änderungsrate“ und der „lokalen Änderungsrate“ genauer erklärt werden. Für Schüler einer FOS oder BOS ist das nicht mehr so wichtig, daher wurden diese Aufgaben an das Ende dieses Kapitels gestellt, obwohl sie eigentlich eine Einführung in das Thema darstellen.

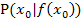 mit dem Differenzialquotienten nach der h-Methode:
mit dem Differenzialquotienten nach der h-Methode: