Die h-Methode
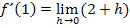
Da jetzt kein h mehr im Nenner steht, kann nun der Grenzwert berechnet werden. D.h. Man kann jetzt endlich h gleich Null setzen. Wir setzen also für h jetzt wirklich genau die Zahl Null ein. Dadurch wird aus der Sekantensteigung genau die Tangentensteigung.
Das Gleichnullsetzen von h klappt nun auch, weil h nach dem Kürzen nicht mehr im Nenner steht und somit der Nenner nicht mehr gleich Null wird, wenn man h gleich Null setzt. Vorher hätten wir h nicht gleich Null setzen können, weil dann eben der Nenner Null ergeben hätte und die Division durch Null bekanntlich nicht definiert ist.
Wir rechnen den Limes aus, indem wir für h die Zahl Null einsetzen:
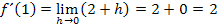
Die Steigung der Tangente an die Funktion 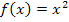 im Punkt
im Punkt 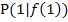 ist daher genau 2.
ist daher genau 2.
Und noch einmal alles allgemein zusammengefasst:
Mit der h-Methode kann die Steigung der Tangente zu einer Funktion 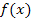 in einem bestimmten Punkt
in einem bestimmten Punkt 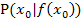 ermittelt werden.
ermittelt werden.
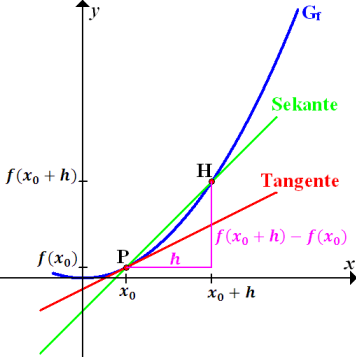
Abb.:Zur h-Methode, in rosa das Steigungsdreieck der Sekante (Der Hilfspunkt H wird immer näher an den festen Punkt P geschoben, d.h. h geht gegen Null, so dass letztendlich aus der Sekante die Tangente und aus der Sekantensteigung die Tangentensteigung wird.)
| Die Grundzüge der h-Methode:
Zur Berechnung der Tangentensteigung einer Funktion Der gegebene Kurvenpunkt hat die Koordinaten Die Sekantensteigung wird dabei mit der folgenden Formel ermittelt: Nun schiebt man den Hilfspunkt H an den gegebenen Punkt Die Tangentensteigung
Das Ergebnis dieses Grenzwertes ist eine Zahl, welche die Steigung der Tangente an den Graph |
Hinweis:Die Berechnung der Ableitung mit Hilfe des Differenzialquotienten, also mit der h-Methode, ist ziemlich umständlich. Zu Beginn musst du die Ableitung einer Funktion leider auf jeden Fall selbständig mit dem Differenzialquotienten berechnen können. Es handelt sich bei der h-Methode allerdings um einen Rechenweg, den du nur momentan brauchst. Später können wir erfreulicherweise komplett darauf verzichten.

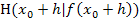 . Vergleiche Abbildung oben! Dabei gilt:
. Vergleiche Abbildung oben! Dabei gilt: 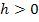
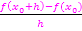
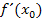 einer Funktion
einer Funktion 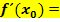
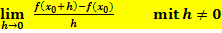
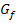 an der Stelle
an der Stelle 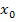 angibt.
angibt.