Die h-Methode
Man nennt dies auch die lokale Änderungsrate von 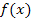 im Punkt P. Auf den Begriff der lokalen Änderungsrate wird im 7. Bsp. und 8. Bsp. weiter unten noch ausführlich eingegangen.
im Punkt P. Auf den Begriff der lokalen Änderungsrate wird im 7. Bsp. und 8. Bsp. weiter unten noch ausführlich eingegangen.
Mit Hilfe des Differenzialquotienten kann die erste Ableitung 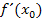 an der Stelle
an der Stelle 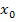 berechnet werden. Mit
berechnet werden. Mit 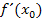 ist nichts anderes als die Tangentensteigung an der Stelle
ist nichts anderes als die Tangentensteigung an der Stelle 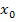 gemeint;
gemeint; 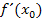 entspricht somit unserer alten Bezeichnung m für die Steigung.
entspricht somit unserer alten Bezeichnung m für die Steigung.
| Wir halten fest:
Die Tangentensteigung im Kurvenpunkt Die Tangentensteigung an der Stelle
Wenn dieser Grenzwert existiert, sagt man:Die Funktion Es gibt aber auch Funktionen, deren Steigung in vereinzelten Punkten nicht berechnet werden kann. Hat eine Funktion beispielsweise einen Knick, kann an dieser Stelle die Steigung der Funktion, also ihre Ableitung, nicht angegeben werden. Dort ist die Funktion nicht differenzierbar. Mehr dazu findest du im Kapitel Stetigkeit und Differenzierbarkeit. |
Nun wollen wir aber endlich besprechen, wie mit Hilfe des Differenzialquotienten die Tangentensteigung 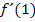 der Funktion
der Funktion 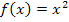 an der Stelle
an der Stelle 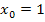 berechnet werden kann.
berechnet werden kann.
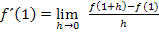
Du weißt: 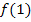 bedeutet, dass für x der Wert 1 in die Funktionsgleichung, also in unserem Beispiel in
bedeutet, dass für x der Wert 1 in die Funktionsgleichung, also in unserem Beispiel in 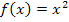 , eingesetzt werden soll.
, eingesetzt werden soll.
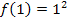
Entsprechend bedeutet 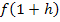 , dass für x der Ausdruck 1 + h in die Funktionsgleichung, also in unserem Beispiel in
, dass für x der Ausdruck 1 + h in die Funktionsgleichung, also in unserem Beispiel in 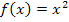 , eingesetzt werden soll.
, eingesetzt werden soll.
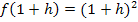
Daher gilt:
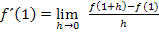
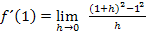
Wir benutzen die erste binomische Formel 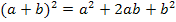 , um die Klammer zu quadrieren:
, um die Klammer zu quadrieren:
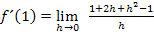
Die Zahlen 1 und -1 im Zähler heben sich weg. Das müssen sie auch unbedingt, weil sie kein h enthalten. Es muss nämlich grundsätzlich alles wegfallen, was kein h enthält. (Sonst könnte man nachher nämlich h nicht ausklammern. Vergleiche nächster Schritt!)
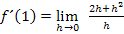
Wir klammern im Zähler h aus, das ergibt:
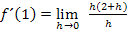
Nun kürzen wir h weg:

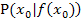 wird auch
wird auch 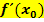
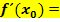
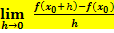
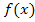 . Die Ableitung
. Die Ableitung 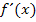 an einer beliebigen Stelle x heißt allgemein „differenzieren“ oder „ableiten“.
an einer beliebigen Stelle x heißt allgemein „differenzieren“ oder „ableiten“.