Die h-Methode
Hier noch einmal die Funktionsgleichung: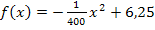 
Allgemeiner Ansatz für die h-Methode:
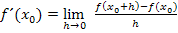
Jetzt müssen wir für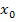 
die x-Koordinate von A, also den Wert -50, einsetzen:
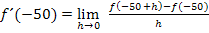
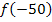müssen wir nicht mehr extra ausrechnen;wir kennen ja die y-Koordinate von A. Deshalb gilt: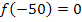 
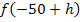bildet man, indem man in der Funktionsgleichung 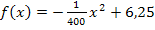für x den Ausdruck -50 + h einsetzt.
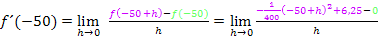
Nun müssen wir den Zähler noch vereinfachen. Dazu verwenden wir die zweite binomische Formel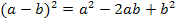 
. Allerdings muss dafür vorher die Reihenfolge in der Klammer umgedreht werden.
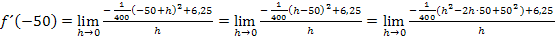
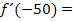
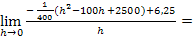
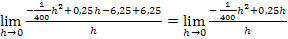
Jetzt lässt sich im Zähler h ausklammern und komplett aus dem Nenner wegkürzen:
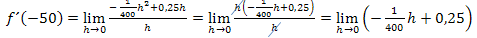
Nun kann der Grenzwert berechnet werden. Man muss nur für h die Zahl 0 einsetzen:
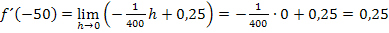
Wieder ergibt sich für die Tangentensteigung im Punkt A der Wert 0,25. Man kann dies übrigens auch in Prozent angeben. Dazu muss man nur das Komma um zwei Stellen nach rechts verschieben. Die Tangente hat somit in A eine Steigung von 25%.
Mit der Formel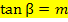 
lässt sich auch der Neigungswinkel 
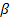der Tangente gegenüber der Horizontalen berechnen, wobei m für die Steigung der Tangente an der Stelle 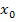steht. Es gilt daher: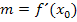 
Zu der Steigung m = 0,25 bzw. m = 25% gehört ein Neigungswinkel 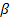von ungefähr 14,04°. Das kannst du selbst folgendermaßen nachrechnen:
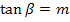
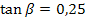
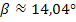
Mit dem Taschenrechner erhältst du mit der Tastenfolge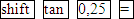 
das oben gezeigte Ergebnis von ungefähr 14,04° für 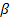. (Achtung:der Taschenrechner muss auf den mode DEG bzw. D für degree/ Grad eingestellt sein!)
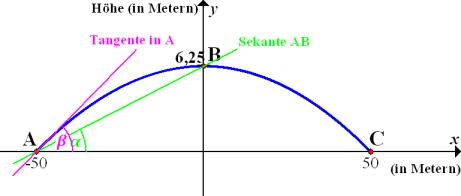
Dies ist jetzt der Winkel, unter dem der Brückenbogen die Horizontale im Punkt A schneidet. Vergleiche dazu die folgende Abbildung!
Abb.: Graph der Parabel 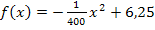mit x 
[-50;50] mit Sekante AB, Neigungswinkel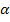 
der Sekante, sowie Tangente im Punkt A und Neigungswinkel der Tangente .
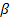Den Neigungswinkel 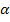der Sekante AB haben wir bereits in Teilaufgabe 7b.) berechnet:
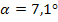
Du siehst, dass der Neigungswinkel 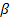der Tangente im Punkt A wesentlich größer ist als der Neigungswinkel 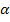der Sekante AB. Will man herausfinden, unter welchem Winkel der Brückenbogen die Horizontale im Punkt A schneidet, darf man also keinesfalls von der durchschnittlichen Steigung zwischen den Punkten A und B ausgehen!
Man muss immer erst die Steigung genau im Punkt A berechnen und nicht die durchschnittliche Steigung zwischen A und B, wenn man den Neigungswinkel der Tangente sucht.
