Die h-Methode
In diesem Zusammenhang bedeutet es nichts anderes als, dass der Hilfspunkt H beliebig nah an P heran geschoben wird. Gleich Null darf h eigentlich nicht werden, denn sonst würde der Nenner gleich Null sein. Wir werden aber nachher einen mathematischen Trick anwenden, so dass h letztendlich doch gleich Null gesetzt werden kann. Erst dadurch wird aus der Sekantensteigung tatsächlich die gesuchte Tangentensteigung.
Bisher wurde die Funktionsgleichung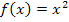 
unseres Einführungsbeispiels noch gar nicht verwendet, weil wir alles noch allgemein geschrieben haben. Die allgemeine Schreibweise ist wichtig, denn wir wollen schließlich letztendlich eine allgemeine Formel für die Tangentensteigung in irgendeinem bestimmten Punkt 
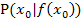einer beliebigen Funktion 
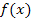herleiten. Bisher wissen wir, dass für die Tangentensteigung im Punkt 
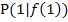gilt:
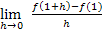
Wenn wir uns nun an Stelle des Beispielpunktes 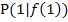mit der x-Koordinate 
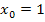einfach einen beliebigen festen Kurvenpunkt 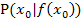vorstellen – d.h. wir ersetzen die konkrete x-Koordinate 1 durch 
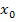– erhalten wir eine allgemeine Formel für die Tangentensteigung in irgendeinem beliebigen Kurvenpunkt 
:
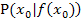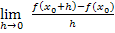
Bei diesem Ausdruck handelt es sich um den Differenzialquotienten an der Stelle 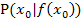. Er entspricht, wie gesagt, der Tangentensteigung einer Funktion 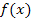im Kurvenpunkt 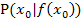. Man nennt dies auch die erste Ableitung 
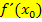an der Stelle .
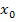Beachte den Unterschied zwischen „Differenzenquotient“ und „Differenzialquotient“! Die beiden Begriffe hören sich zwar sehr ähnlich an, bedeuten aber etwas ganz anderes:
Der Differenzenquotient ist nur der Ausdruck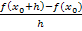 
alleine ohne limes;er beschreibt die Sekantensteigung, d.h. die mittlere (durchschnittliche) Steigung der Funktion 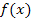zwischen den zwei Punkten P und H. Die mittlere Steigung ist die durchschnittliche Änderung des Funktionswertes 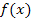zwischen P und H im Vergleich zur Änderung von x. Der Differenzenquotient gibt daher an, um wie viel der Funktionswert 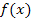im Vergleich zu x in diesem Intervall zunimmt bzw. abnimmt. Man nennt dies auch die mittlere Änderungsrate von 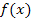zwischen den Punkten P und H. Der Begriff der mittleren Änderungsrate wird nachher im 6. Bsp. und 7. Bsp. noch ausführlich erläutert.
Der Differenzialquotient ist dagegen der Ausdruck 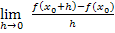also mit limes. Er beschreibt die Tangentensteigung in einem bestimmten Kurvenpunkt P, d.h. die lokale Steigung der Funktion im Punkt P. Es geht darum, wie steil bzw. flach die Kurve in diesem einen Punkt ist, also wie stark sich der Funktionswert 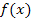im Vergleich zu x ändert, aber nicht in einem Intervall, sondern nur in einem Punkt.
