Die h-Methode
Da man durch einen Bruch dividiert, indem man mit dem Kehrwert multipliziert, kann an Stelle der Division durch den Bruch 
auch eine Multiplikation mit dem Kehrbruch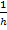 
vorgenommen werden. Das geht dann folgendermaßen:
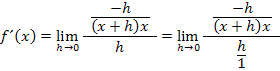
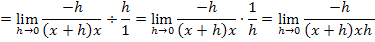
Jetzt kann h weggekürzt und der Grenzwert berechnet werden:
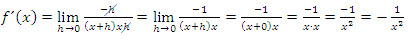
Somit haben wir die Ableitungsfunktion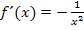 
der Funktion 
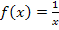ermittelt.
Zu 5b.)
Es soll die Gleichung der Tangente im Kurvenpunkt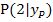 
an die Funktion 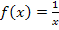berechnet werden. Da eine Tangente eine Gerade ist, gilt für sie auch die allgemeine Geradengleichung y = mx + t, mit der Steigung m und dem y-Achsenabschnitt t.
Als erstes berechnen wir die y-Koordinate des Punktes P. (Wir brauchen diese y-Koordinate nachher bei der Berechnung des y-Achsenabschnitts t der Tangente. Es ist in der Aufgabe schließlich nicht nur nach der Tangentensteigung, sondern nach der gesamten Tangentengleichung gefragt.) Weil P ein Punkt des Graphen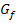 
ist, erhalten wir seine y-Koordinate, indem wir die x-Koordinate von P in die Funktionsgleichung 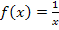einsetzen:
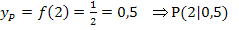
Als nächstes müssen wir die Steigung m der Tangente im Punkt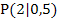 
ermitteln. (Wir brauchen auch sie später bei der Berechnung des y-Achsenabschnitts t.) Die Tangentensteigung erhalten wir durch das Einsetzen von x = 2 in die Ableitungsfunktion 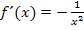. Es gilt somit für die Tangentensteigung:
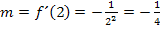
Den y-Achsenabschnitt t erhält man, wenn man die Koordinaten des Punktes 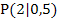für x bzw. y und den soeben berechneten Wert für m einsetzt und nach t auflöst.
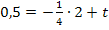
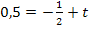
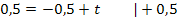
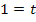
Die Gleichung der Tangente im Punkt P lautet daher: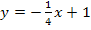 
Fertig!
In den nächsten Beispielen wollen wir uns mit Anwendungsaufgaben des Differenzen- und des Differenzialquotienten beschäftigen. Für Schüler einer 11. Klasse des G8 ist dies besonders wichtig. Die Begriffe Differenzen- und Differenzialquotient lassen sich ja anschaulich nicht nur als Sekanten- und Tangentensteigung deuten, sondern auch als „mittlere Änderungsrate“ und „lokale Änderungsrate“. Was die Begriffe „mittlere Änderungsrate“ und „lokale Änderungsrate“ genau bedeuten, wird an Hand der folgenden Beispiele herausgearbeitet.
6. Bsp.:Wertentwicklung einer Aktie
Der folgende Graph zeigt die Wertentwicklung einer Aktie seit Öffnung der Börse um 8 Uhr bis zum Schluss der Börse um 16 Uhr. x ist die Zeit in Stunden seit Öffnung der Börse.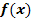 
ist der Wert der Aktie in €.
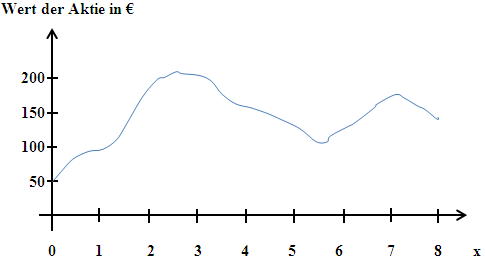
In der folgenden Tabelle kannst du den Wert der Aktie jeweils zur vollen Stunde ablesen:
| x in Std. | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Wert f(x) in € | 50 | 98 | 182 | 198 | 169 | 146 | 139 | 172 | 152 |
