Die h-Methode

Die Ableitungsfunktion ist an der Stelle x = 0 nicht definiert;die Funktion selbst ist dagegen an dieser Stelle sehr wohl definiert. An der Stelle x = 0 lässt sich die Ableitung 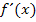also nicht berechnen, obwohl die Funktion selbst dort definiert ist. Man sagt:Die Funktion 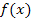ist an der Stelle x = 0 nicht differenzierbar. Das bedeutet, dass an dieser Stelle die Steigung der Funktion nicht berechnet werden kann. Das liegt in diesem Fall daran, dass die Tangente an die Wurzelfunktion 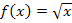bei x = 0 senkrecht verläuft. Ihre Steigung wäre demnach unendlich groß. Betrachte dazu die folgende Abbildung!

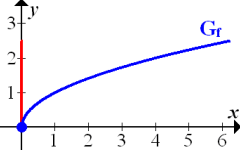
Abb.:  Graph der Wurzelfunktion 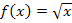mit senkrechter Tangente (rot) im Punkt (0|0)

Damit sind wir mit dieser Aufgabe fertig! Den Trick mit dem Erweitern zur dritten binomischen Formel bei der Berechnung des Differenzialquotienten einer Funktion mit Wurzel solltest du dir gut merken.

Und gleich noch ein interessantes Beispiel:

5. Bsp.:

Gegeben ist die Funktion 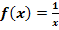mit ihrer maximalen Definitionsmenge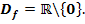

a.) Berechne die Ableitungsfunktion 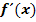mit Hilfe des Differenzialquotienten!

b.) Ermittle die Gleichung der Tangente an den Graph 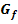im Kurvenpunkt !

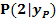Lösung:

Zu 5a.)

Es soll die Ableitungsfunktion 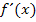mit Hilfe des Differenzialquotienten ermittelt werden, d.h. wir sollen die Ableitung mit der h-Methode berechnen und außerdem 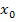durch x ersetzen. Allgemeiner Ansatz für die h-Methode:

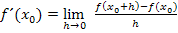
Dieses Mal ersetzen wir gleich zu Beginn 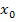durch x. (Du kannst das natürlich auch erst am Ende deiner Rechnung machen. Es soll hier nur auch einmal anders herum gezeigt werden.)

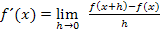
Versuche es doch ´mal alleine, den Differenzialquotienten für die Funktion 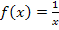zu bilden!

Zur Erinnerung: 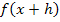bildest du, indem du für x in die Funktionsgleichung x + h einsetzt.

Hast du es selbst probiert? Dann müsstest du eigentlich zu folgendem Ergebnis gekommen sein:

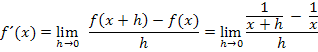
Nun muss das Ganze aber noch so umgeformt werden, dass sich h wieder herauskürzen lässt. Als erstes bringen wir die beiden Brüche im Zähler des Differenzialquotienten auf einen gemeinsamen Nenner. Der Hauptnenner ist natürlich 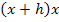, deshalb muss der erste Bruch mit x und der zweite Bruch mit (x + h) erweitert werden.

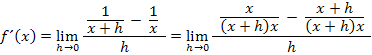
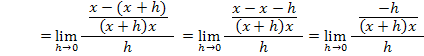
Nun wollen wir den Doppelbruch beseitigen. Dazu stellen wir uns den Hauptbruchstrich (den längsten Bruchstrich) als 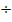vor. Statt dem h im Nenner kann man sich auch den Bruch denken.

---