Delta-x-Methode
(Es gibt jetzt schließlich keinen Nenner mehr, der Null werden könnte. Vor dem Kürzen hätte man 
noch nicht gleich Null setzen können, denn dann wäre der Nenner gleich Null geworden und das ist schließlich nicht definiert. Deshalb ist das vorherige Ausklammern und anschließende Kürzen von unerlässlich.)
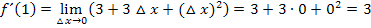
Die Steigung der Funktion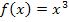 
an der Stelle 
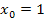ist somit 3.
Fertig!
Kleiner Tipp:
Wenn du bei ein und derselben Funktion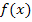 
in mehreren verschiedenen Punkten, also an mehreren Stellen 
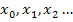die Tangentensteigung berechnen sollst, empfiehlt es sich, nicht gleich zu Beginn der Rechnung für 
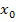eine der konkreten Zahlen in den Differenzialquotienten einzusetzen, das durch zurechnen und danach die x-Koordinate des nächsten Punktes einzusetzen, wieder alles durchzurechnen usw.. Dann müsste man ja mehrmals den kompletten Differenzialquotienten zwar mit der gleichen Funktion, aber mit verschiedenen Zahlen 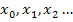berechnen und das wäre sehr viel Arbeit. Geschickter ist es dann, den Differenzialquotienten erst allgemein mit 
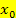zu berechnen, also vorerst nichts für 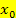einzusetzen. Im Ergebnis der Ableitung 
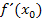kommt dann in der Regel noch 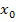vor. Erst in dieses Ergebnis setzt du dann nacheinander die gegebenen Werte 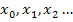für 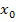ein, um jeweils die Tangentensteigung an diesen Stellen zu erhalten. Dazu das nächste Beispiel!
3. Bsp.:
Gegeben ist die Funktion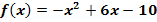 
. Es soll die Steigung der Funktion in den Punkten P(2|f(2)), Q(3|f(3)) und R(4|f(4)) berechnet werden. Ermittle dazu erst die Tangentensteigung in einem beliebigen Kurvenpunkt ( 
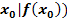und setze danach für 
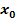die Werte 2, 3 und 4 ein!
Lösung:
Um Zeit zu sparen, wird in dieser Aufgabe nicht dreimal nacheinander der Differenzialquotient für die einzelnen Werte von 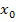gebildet, sondern nur einmal mit dem allgemeinen Kurvenpunkt ( 
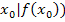. Wir rechnen also nicht mit einer echten Zahl, sondern einfach allgemein mit 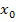. Dadurch erhalten wir die Ableitung 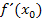. Danach können dann die entsprechenden Werte 2, 3 und 4 nacheinander für 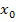in die Ableitung eingesetzt werden. Versuch´s doch gleich mal selbst, ohne dir die folgende Lösung anzuschauen! Du musst hier im Prinzip genauso rechnen, wie in den vorherigen Beispielen, nur dass du dieses Mal nicht gleich zu Beginn eine konkrete Zahl für 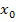einsetzt. Das Einsetzen der Zahlen 2, 3 und 4 heben wir uns erst einmal für später auf.
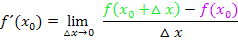
Falls du jetzt nicht weiter weißt:
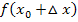berechnet man, indem man in der Funktionsgleichung 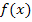an Stelle von jedem x den Ausdruck 
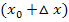schreibt. 
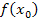erhältst du dadurch, dass du in der Funktionsgleichung statt x einfach 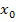schreibst.
