Delta-x-Methode
Dazu müssen wir aber die Reihenfolge in der Klammer umdrehen: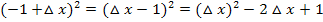 
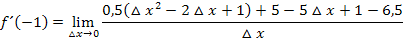
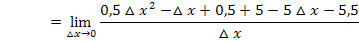
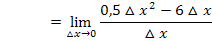
Nun kann im Zähler 
ausgeklammert und im nächsten Schritt weggekürzt werden. Durch das Ausklammern entsteht im Zähler ein Produkt, so dass man dann kürzen darf. Vor dem Ausklammern von darf nicht gekürzt werden, denn im Zähler liegt eine Differenz vor und aus Differenzen und Summen darf nicht gekürzt werden. Das weißt du bestimmt selbst. (Wenn sich im Zähler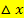 
nicht ausklammern lässt, weil im Zähler noch eine Zahl ohne 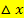vorkommt, hast du dich sicher verrechnet! 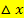muss sich ausklammern und nachher wegkürzen lassen, sonst ist deine Rechnung falsch.)
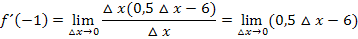
Nun kann der Grenzwert berechnet werden, indem gleich Null gesetzt wird. (Es gibt jetzt schließlich keinen Nenner mehr, der Null werden könnte.)
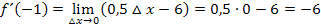
Die Steigung der Tangente im Punkt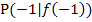 
an die Funktion 
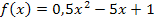ist somit -6.
Und zur Übung gleich noch eine weitere Beispielaufgabe. Du kannst sie gleich ´mal alleine probieren und dann erst mit der Lösung vergleichen.
2. Bsp.:
Berechne die Steigung der Funktion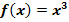 
an der Stelle 
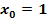mit Hilfe des Differenzialquotienten!
Lösung:
Geg.: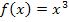 
Die Steigung der Funktion an der Stelle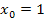 
entspricht der Tangentensteigung im Punkt 
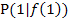. Wir gehen vom Prinzip her wie im 1. Bsp. vor.
Wir verwenden den allgemeinen Ansatz für den Differenzialquotienten:
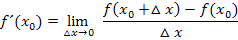
In diesem Beispiel ist 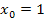. Daher setzen wir für 
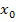die Zahl 1 in den allgemeinen Ansatz ein:
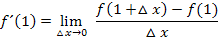
Wir bilden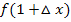 
und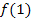 
, indem wir für jedes x den Ausdruck 
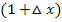bzw. die Zahl 1 in die Funktionsgleichung 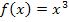einsetzen. So ergibt sich:
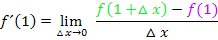
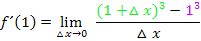
Um die Klammer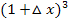 
auszurechnen, kannst du entweder 
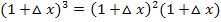rechnen oder die Formel 
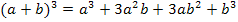verwenden. Diese Formel kann man sich mit Hilfe des Pascalschen Dreiecks herleiten. Wir haben hier die zuletzt gezeigte Formel angewendet, weil es schneller geht als mit binomischer Formel und anschließendem Ausmultiplizieren.
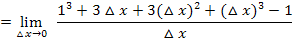
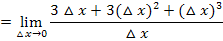
Wie es nun weiter geht, müsstest du inzwischen eigentlich schon wissen.
Was kommt denn immer als nächster Schritt, nachdem man im Zähler alles soweit möglich zusammengefasst hat?
Bist du selbst d´raufgekommen?
Richtig! kann nun im Zähler ausgeklammert und im nächsten Schritt weggekürzt werden.
Wir klammern also im Zähler aus, das ergibt dann:
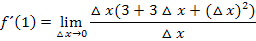
Kürzen mit ergibt:
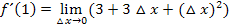
Nun kann der Grenzwert endlich berechnet werden, indem man für die Zahl Null einsetzt.
