Delta-x-Methode

Wenn in einer Aufgabe steht, dass du eine Funktion in einem Punkt 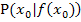„lokal differenzieren“ sollst, dann heißt das so viel wie:„Berechne die Tangentensteigung der Funktion im Punkt 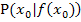“. Du musst dann die Ableitung 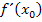berechnen. Den Differenzialquotienten musst du dabei nur zu Beginn des Themas Differenzialrechnung verwenden, solange du die sogenannten Ableitungsregeln noch nicht gelernt hast, oder wenn in der Aufgabe explizit steht, dass der Differenzialquotient verwendet werden soll. Später geht das Ableiten wesentlich schneller auch ohne langwieriger Berechnung des Differenzialquotienten. (Dazu mehr bei:Einfache Ableitungsregeln)

Du solltest die Berechnung der Ableitung 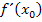an einer bestimmten Stelle 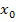mit dem Differenzialquotienten jedoch trotzdem gut üben, denn in der Schulaufgabe zu diesem Stoff wird das bestimmt verlangt und bringt richtig viele Punkte – wenn man es kann. Die Berechnung des Differenzialquotienten dauert schließlich ziemlich lange und ist ja nicht ganz ohne. Manchmal kommt dies sogar schon vor der entsprechenden Schulaufgabe in einer Ex dran!

Nun folgen einige konkrete Beispiele für die Berechnung der Tangentensteigung mit dem Differenzialquotienten. Im 1. bis 5. Beispiel wird jeweils die Delta-x-Methode an einigen etwas schwierigeren Beispielen vorgeführt. Ab dem 6. Bsp. kommen die besonders für G8 Schüler extrem wichtigen Anwendungsaufgaben, an Hand derer auch die Begriffe der „mittleren Änderungsrate“ und der „lokalen Änderungsrate“ genauer erklärt werden. Für Schüler einer FOS oder BOS ist das nicht mehr so wichtig, daher wurden diese Aufgaben an das Ende dieses Kapitels gestellt, obwohl sie eigentlich eine Einführung in das Thema darstellen.

1. Bsp.:Eine typische Aufgabe zum Differenzialquotienten

Berechne die Steigung der Tangente an die Funktion 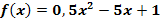im Punkt 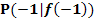mit Hilfe des Differenzialquotienten!

Lösung:

Die Steigung der Tangente im Punkt 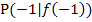ist die erste Ableitung 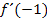. Die Funktion 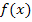muss demnach an der Stelle 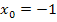abgeleitet bzw. differenziert werden. Wir müssen also 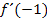bilden.

Wir verwenden den allgemeinen Ansatz des Differenzialquotienten, d.h. die Delta-x-Methode:

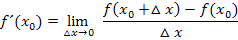
In diesem Beispiel hat der Punkt P die x-Koordinate 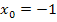. Wir setzen deshalb für 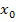die Zahl -1 in den allgemeinen Ansatz ein:

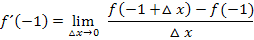
Wir bilden 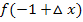und 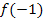, indem wir für jedes x den Ausdruck 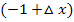bzw. die Zahl -1 in die Funktionsgleichung 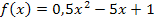einsetzen. So ergibt sich:

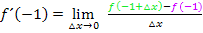
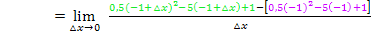
Um die Klammer 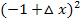auszurechnen, verwenden wir die zweite binomische Formel .

---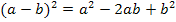