Delta-x-Methode
Dies entspricht dem Differenzialquotienten der Funktion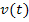 
.
Der Differenzialquotient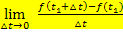 
bzw. 
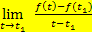gibt hier somit die momentane Änderungsrate der Geschwindigkeit, also die momentane Beschleunigung 
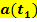zum Zeitpunkt 
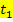an.
In der Lösung von Teilaufgabe 8d.) kannst du sehen, wie die momentane Beschleunigung des Sportwagens nach genau 3 Sekunden berechnet werden kann.
Zu 8c.)
Es soll die mittlere Beschleunigung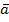 
innerhalb der ersten bis zur dritten Sekunde, also die durchschnittliche Geschwindigkeitsänderung im Vergleich zur dafür benötigten Zeit, berechnet werden.
Dies entspricht dem Differenzenquotienten der Funktion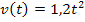 
für t 
[1;3].
Hier noch einmal die benötigten Daten, die wir schon für die Wertetabelle berechnet haben:
Mittlere Beschleunigung für t [1;3]:
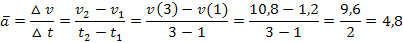
Die mittlere Beschleunigung 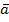innerhalb der ersten bis zur dritten Sekunde beträgt 
.
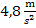Zu 8d.)
Wir sollen in dieser Teilaufgabe die momentane Beschleunigung nach 3 Sekunden Fahrt ermitteln, also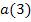 
. Dies entspricht dem Differenzialquotienten der Funktion 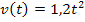zum Zeitpunkt 
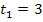. Der Differenzialquotient lässt sich auf zwei verschiedene Weisen schreiben:
Momentane Beschleunigung zum Zeitpunkt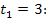 
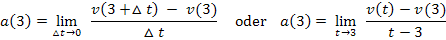
Daher gibt es auch zwei verschiedene Rechenwege.
1. Variante:
Wir arbeiten mit dem Ansatz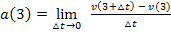 
. Du erkennst bestimmt, dass es sich um den Ansatz des Differenzialquotienten der Delta-x-Methode handelt. Das 
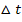entspricht hierbei einfach dem 
aus der Delta-x-Methode;da in dieser Aufgabe die Variable nicht x sondern t heißt.
Um 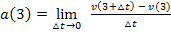zu berechnen, benötigen wir 
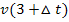und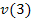 
.
Den Wert v(3) kennen wir schon:v(3) = 10,8.
Den Ausdruck 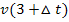müssen wir noch bilden, indem wir 
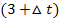für t in die Funktionsgleichung 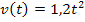einsetzen.
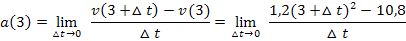
Wir vereinfachen nun den Zähler soweit möglich. Dazu benützen wir die erste binomische Formel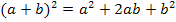 
, dann fassen wir zusammen und klammern 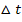aus, damit sich letztlich 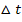kürzen lässt und der Grenzwert berechnet werden kann. So geht man schließlich immer bei der Berechnung des Differenzialquotienten vor.
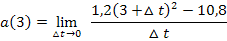
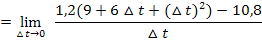
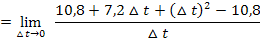
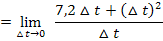
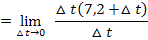
Nun lässt mit 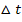kürzen:
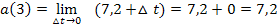
Die momentane Beschleunigung zum Zeitpunkt 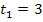beträgt somit 
.
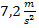2. Variante:
Wir nehmen den anderen Ansatz des Differenzialquotienten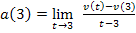 
mit t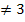 
. Dafür braucht man 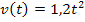und v(3) = 10,8. Eingesetzt ergibt dies:
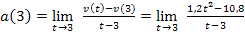
Im Zähler klammern wir den Faktor 1,2 aus. Dadurch ergibt sich in der Klammer ein Term, der sich mit der dritten binomischen Formelumformen lässt.
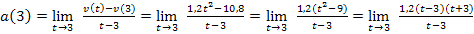
Wie es jetzt weiter geht, ist dir sicherlich klar.
