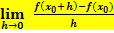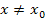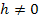Delta-x-Methode
Fassen wir zum Abschluss dieses Beispiels noch einmal kurz zusammen, was du daran lernen solltest:
| Von der mittleren Änderungsrate, also der Sekantensteigung, ist die lokale Änderungsrate in einem Punkt, also die Tangentensteigung in diesem einen Kurvenpunkt, zu unterscheiden:
Mittlere Änderungsrate (Sekantensteigung zwischen
Lokale Änderungsrate (Tangentensteigung in
|
Nun zum nächsten Beispiel.
8. Bsp.:Beschleunigung
Ein Auto beschleunigt aus dem Stand. Seine Geschwindigkeit 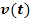 in
in 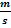 nach t Sekunden kann mit Hilfe der Zeit-Geschwindigkeitsfunktion
nach t Sekunden kann mit Hilfe der Zeit-Geschwindigkeitsfunktion 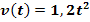 berechnet werden, welche zumindest für eine gewisse Zeit den Zusammenhang zwischen der vergangenen Zeit t (in Sekunden) und der erreichten Geschwindigkeit v (in
berechnet werden, welche zumindest für eine gewisse Zeit den Zusammenhang zwischen der vergangenen Zeit t (in Sekunden) und der erreichten Geschwindigkeit v (in 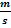 ) beschreibt.
) beschreibt.
a.) Erstelle eine Wertetabelle für die ersten vier Sekunden in Schritten von 0,5 Sekunden und zeichne den Graph für 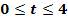 . (Maßstab:t- Achse:1 cm = 0,5 Sekunden;v- Achse:1 cm = 5
. (Maßstab:t- Achse:1 cm = 0,5 Sekunden;v- Achse:1 cm = 5 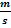 )
)
b.) Erkläre an diesem Beispiel, was man unter der absoluten Änderung der Geschwindigkeit und der mittleren Änderung der Geschwindigkeit versteht. Wodurch unterscheidet sich davon die momentane Änderung der Geschwindigkeit? Was bedeuten in diesem Zusammenhang die Begriffe „Differenzenquotient“ und „Differenzialquotient“ anschaulich?
c.) Berechne die mittlere Beschleunigung des Autos von der ersten bis zur dritten Sekunde.
d.) Welche momentane Beschleunigung wirkt auf das Auto genau 3 Sekunden nach dem Start?
Lösung:
Zu 8a.)
Das Erstellen der Wertetabelle und das Zeichnen des Funktionsgraphen dürfte kein Problem für dich darstellen. Daher keine weitere Erklärung dazu.
Wertetabelle zu 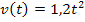 für
für 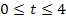 mit △t = 0,5
mit △t = 0,5
| t in s | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 |
v in  |
0 | 0,3 | 1,2 | 2,7 | 4,8 | 7,5 | 10,8 | 12,25 | 19,2 |
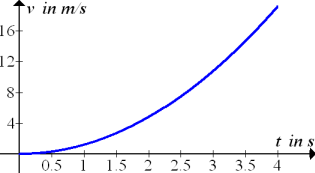
Abb.:Graph der Funktion 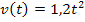 für
für 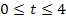
Zu 8b.)
Die Änderung 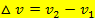 bezeichnet man als absolute Änderung der Geschwindigkeit. Sie gibt an, wie stark sich die Geschwindigkeit des Autos innerhalb eines bestimmten Zeitintervalls ändert, aber nicht in Bezug auf die dabei vergangene Zeit △t. Die absolute Änderung der Geschwindigkeit hat die gleiche Einheit wie die Geschwindigkeit v, also in diesem Fall die Einheit
bezeichnet man als absolute Änderung der Geschwindigkeit. Sie gibt an, wie stark sich die Geschwindigkeit des Autos innerhalb eines bestimmten Zeitintervalls ändert, aber nicht in Bezug auf die dabei vergangene Zeit △t. Die absolute Änderung der Geschwindigkeit hat die gleiche Einheit wie die Geschwindigkeit v, also in diesem Fall die Einheit  .
.

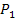 und
und 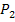 )
) 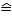 Differenzenquotient
Differenzenquotient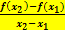
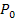 )
) 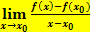 bzw.
bzw.