Delta-x-Methode
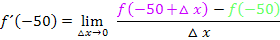
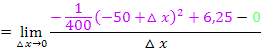
Nun müssen wir den Zähler noch vereinfachen. Dazu verwenden wir die zweite binomische Formel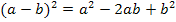 
. Allerdings muss dafür vorher die Reihenfolge in der Klammer umgedreht werden.
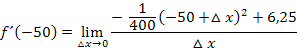
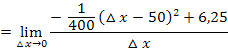
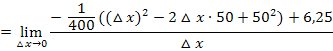
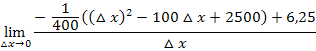
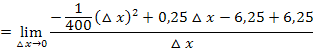
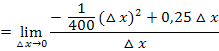
Jetzt lässt sich im Zähler 
ausklammern und komplett aus dem Nenner wegkürzen:
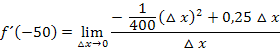
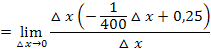
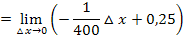
Nun kann der Grenzwert berechnet werden. Man muss nur für die Zahl 0 einsetzen:
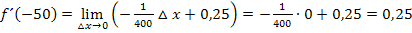
Wieder ergibt sich für die Tangentensteigung im Punkt A der Wert 0,25. Man kann dies übrigens auch in Prozent angeben. Dazu muss man nur das Komma um zwei Stellen nach rechts verschieben. Die Tangente hat somit in A eine Steigung von 25%.
Mit der Formel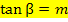 
lässt sich auch der Neigungswinkel 
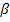der Tangente gegenüber der Horizontalen berechnen, wobei m für die Steigung der Tangente an der Stelle 
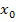steht. Es gilt daher: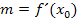 
Zu der Steigung m = 0,25 bzw. m = 25% gehört ein Neigungswinkel 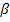von ungefähr 14,04°. Das kannst du selbst folgendermaßen nachrechnen:
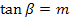
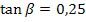
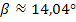
Mit dem Taschenrechner erhältst du mit der Tastenfolge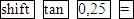 
das oben gezeigte Ergebnis von ungefähr 14,04° für 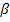. (Achtung:der Taschenrechner muss auf den mode DEG bzw. D für degree/ Grad eingestellt sein!)
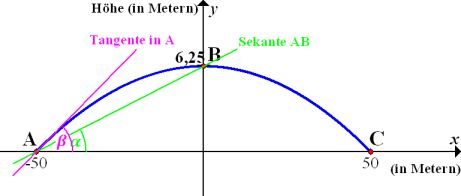
Dies ist jetzt der Winkel, unter dem der Brückenbogen die Horizontale im Punkt A schneidet. Vergleiche dazu die folgende Abbildung!
Abb.: Graph der Parabel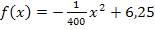 
mit x 
[-50;50] mit Sekante AB, Neigungswinkel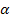 
der Sekante, sowie Tangente im Punkt A und Neigungswinkel der Tangente .
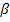Den Neigungswinkel 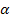der Sekante AB haben wir bereits in Teilaufgabe 7b.) berechnet:
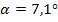
Du siehst, dass der Neigungswinkel 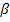der Tangente im Punkt A wesentlich größer ist als der Neigungswinkel 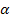der Sekante AB. Will man herausfinden, unter welchem Winkel der Brückenbogen die Horizontale im Punkt A schneidet, darf man also keinesfalls von der durchschnittlichen Steigung zwischen den Punkten A und B ausgehen!
Man muss immer erst die Steigung genau im Punkt A berechnen und nicht die durchschnittliche Steigung zwischen A und B. Da die Brücke zuerst steiler und dann immer flacher wird, kann ein durchschnittlicher Wert der Steigung keine Hilfe bei der genauen Berechnung des Neigungswinkels der Brücke in einem bestimmten Punkt sein. Daher ist die Tangentensteigung, d.h. die lokale Änderungsrate des Funktionswertes, unerlässlich für die Berechnung des Neigungswinkels einer Kurve in einem bestimmten Kurvenpunkt. Daran kannst du die Wichtigkeit des Differenzialquotienten erahnen.
