Delta-x-Methode

Tangentensteigung im Punkt A:        (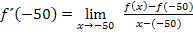

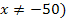
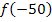müssen wir nicht mehr berechnen, da dies ja der y-Koordinate des Punktes A(-50|0) entspricht. Deshalb gilt: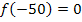

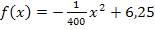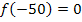Einsetzen der Funktionsgleichung und in unseren Ansatz des Differenzialquotienten ergibt:

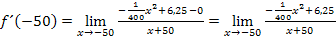
Nun müssen wir den Grenzwert aber noch ausrechnen. In der momentan vorliegenden Form kann für x der Wert -50 noch nicht eingesetzt werden, da der Nenner gleich Null werden würde. Um den Grenzwert zu berechnen, müssen wir aber für x genau den Wert -50 einsetzen können. Daher muss vorher derart umgeformt werden, dass sich x + 50 wegkürzen lässt. Erst danach kann der Grenzwert durch Einsetzen von x = -50 berechnet werden. Also, los geht´s mit den Umformungen!

Im Zähler klammern wir erst einmal den Faktor 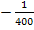aus. Warum? Das wird dir sicher gleich von selbst klar.

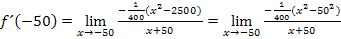
Hast du erkannt, was nun im Zähler vorliegt?

Richtig! Eine binomische Formel! Und welche ist es? Klar, die dritte binomische Formel!

Nach dem Ausklammern des Bruchs erkennt man doch wesentlich leichter, dass im Zähler die dritte binomische Formel vorliegt. Durch die Anwendung der binomischen Formel kann man den Zähler dann so umformen, dass sich x + 50 kürzen und anschließend der Grenzwert berechnen lässt. (Aus genau diesem Grund wurde vorher ausgeklammert.)

Zur Erinnerung:          Dritte binomische Formel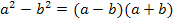       

Damit ergibt sich:

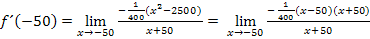
Nun können wir endlich den Faktor x + 50 wegkürzen.

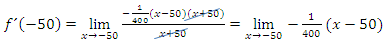
Jetzt kann der Grenzwert leicht berechnet werden:Man braucht nur für x den Wert -50 einsetzen. Es gibt ja nun keinen Nenner mehr, der Null ergeben könnte. Also gibt es auch kein Problem mehr bei der Berechnung des Grenzwertes.

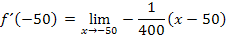
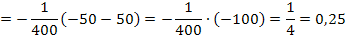
Wie schon erwartet, ergibt sich für die Tangentensteigung im Punkt A der Wert 0,25.

2. Variante (Delta-x-Methode)

Diese Variante unterscheidet sich von der soeben vorgestellten 1. Variante nur in der Wahl der Schreibweise des Hilfspunktes H. Der Punkt A(-50|0) ist gegeben. Der Hilfspunkt H hat eine um größere x-Koordinate als A. Daher gilt: 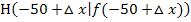. Du hast jetzt bestimmt erkannt, dass wir bei dieser Variante die Delta-x-Methode anwenden wollen. Also los geht´s!

Hier noch einmal die Funktionsgleichung: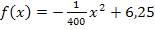   

Allgemeiner Ansatz:

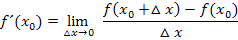
Jetzt müssen wir für 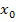die x-Koordinate von A, also den Wert -50, einsetzen:

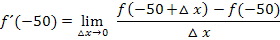
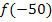müssen wir nicht mehr extra ausrechnen;wir kennen ja die y-Koordinate von A. Deshalb gilt: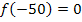

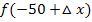bildet man, indem man in der Funktionsgleichung 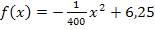für x den Ausdruck 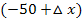einsetzt.

---