Delta-x-Methode
Er liegt sehr nahe an A. Die x-Koordinaten von A und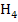 
unterscheiden sich nur noch um 0,01.
Jetzt bilden wir den Differenzenquotienten, um die mittlere Höhenänderung zwischen A und 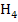, d.h. die Sekantensteigung, zu berechnen: A(-50;0) und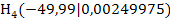 
Sekantensteigung zwischen A und :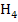 
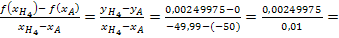
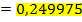
Nun überlege dir doch einmal, an welchen Wert sich die Sekantensteigung annähert, wenn man mit den Hilfspunkten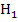 
, 
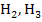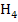und immer näher an A heran rückt. (Am weitesten von A entfernt liegt ja 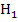, etwas näher an A ist da schon 
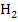, noch näher an A liegt 
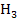und am nächsten bei A liegt .)
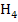Betrachte nun noch einmal die oben berechneten Werte der Sekantensteigung bei A und 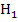, 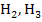sowie :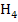
Sekantensteigung zwischen A und :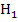 
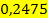
Sekantensteigung zwischen A und :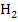 
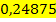
Sekantensteigung zwischen A und :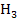 
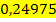
Sekantensteigung zwischen A und :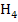 
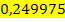
An welche Zahl nähert sich die Sekantensteigung wohl an?
Du hast bestimmt gemerkt, dass sich die Ergebnisse der Sekantensteigung immer mehr an den Wert 0,25 annähern. Umso kleiner der Abstand der Hilfspunkte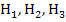 
bzw. 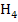vom Punkt A wird, desto kleiner wird auch die Abweichung der Tangentensteigung von der Sekantensteigung. Wenn man den Hilfspunkt H immer näher an A heranschiebt, wird aus der Sekante letztendlich die Tangente im Punkt A. Aus der Sekantensteigung wird dann natürlich die Tangentensteigung im Punkt A. Wir vermuten daher, dass die Tangente im Punkt A genau die Steigung 0,25 hat. Dies entspricht auch der Steigung der Funktion 
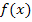im Punkt A bzw. der lokalen Änderungsrate des Funktionswertes in diesem Punkt. Genau das wollen wir jetzt berechnen.
Um die Steigung der Kurve, d.h. die Tangentensteigung bzw. die lokale Änderungsrate, im Punkt A zu berechnen, müssen wir den Differenzialquotienten bilden und den Grenzwert berechnen. Man sagt auch, dass man die Tangentensteigung durch „Grenzübergang“ berechnet. Das bedeutet nur, dass man den Grenzwert des Differenzialquotienten berechnen soll. Wir können dies auf zwei verschiedene Art und Weisen machen:
1. Variante
Wir legen durch den festen Punkt A(-50|0) und durch den Hilfspunkt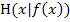 
die Sekante. Dann schieben wir H beliebig nah an A heran. D.h. in diesem Fall, wir schieben x immer näher an die x-Koordinate des Punktes A, also an -50, heran. Damit wird aus der Sekantensteigung (der mittleren Änderungsrate der Höhe) die Tangentensteigung (die lokale Änderungsrate der Höhe) im Punkt A. Das Heranschieben von x an -50 drücken wir mathematisch durch den Grenzwert 
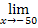… aus.
